Контрольні завдання по дисципліні “Випадкові процеси”
Задача 1.Двовимірний закон розподілу випадкової величини ( надалі ВВ ) ![]() записується щільністю:
записується щільністю: 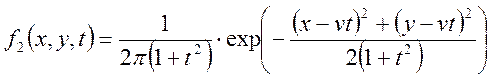 .
.
Знайти усі імовірностні характеристики.
Задача 2. ВВ є часткою случаємо такої випадкової функції, у якого
відсутня залежність від часу ![]() :
: ![]() і
описується показовим законом
і
описується показовим законом
розподілу, з ![]() (
(![]() ). Знайти:
). Знайти: ![]() ,
, ![]() ,
, ![]() .
.
Задача 3.Випадковий процес має вигляд ![]() ,
, ![]() .
. ![]() — ВB, рівномірно розподілена на відрізку [0,3].
Знайти одномірну функцію і щільність розподілу.
— ВB, рівномірно розподілена на відрізку [0,3].
Знайти одномірну функцію і щільність розподілу.
Задача 4.ВВ
задана у виді ![]() .
. ![]() — ВВ, що підкоряється нормальному
законові з
параметрами
— ВВ, що підкоряється нормальному
законові з
параметрами ![]() ,
, ![]() .
. ![]() —
невипадкова константа. Знайти одномірну щільність
—
невипадкова константа. Знайти одномірну щільність ![]() і
і ![]() ,
, ![]() ,
, ![]() .
.
Задача 5.Випадкова функція ![]() ,де
,де ![]() і
і ![]() —незалежні ВВ, що підкоряються
тому самому нормальному законові розподілу
—незалежні ВВ, що підкоряються
тому самому нормальному законові розподілу ![]() . Використовуючи властивості математичного чекання
і дисперсії обчислити
. Використовуючи властивості математичного чекання
і дисперсії обчислити ![]() ,
, ![]() ,
, ![]() і одномірну щільність
і одномірну щільність ![]() .
.
Задача 6.Задано дві щільності ![]() і
і
![]() двох
випадкових незалежних ВВ
двох
випадкових незалежних ВВ ![]() і
і ![]() .
Записати одномірну щільність
.
Записати одномірну щільність ![]() процесу
процесу ![]() ,
, ![]() .
.
Задача 7.Випадковий процес заданий у виді ![]() ,де
,де ![]() і
і ![]() — ВВ з параметрами
— ВВ з параметрами ![]() ,
, ![]() .
Знайти
.
Знайти ![]() ,
, ![]() ,
, ![]() ,
, ![]() , де
, де 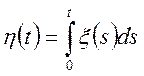 .
.
Задача 8.Випадковий процес заданий у виді ![]() , де
, де ![]() — ВB з
— ВB з ![]() ,
, ![]() .
.
Знайти імовірностні характеристики
випадкового процесу 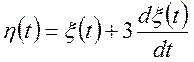 .
.
Задача 9. Матеріальна крапка може знаходитися або у вершинах трикутника ABC (мал.1), або переміщатися від однієї вершини
до іншої в зазначених на малюнку напрямках з відповідними імовірностями: b к. A — з імовірністю ![]() в к. B —
в к. B — 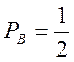 ; b к. C—
; b к. C— 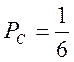 ; переміщатися
від C до A з імовірністю
; переміщатися
від C до A з імовірністю 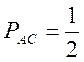 , від C до B—
, від C до B— 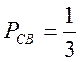 , від B до A—
, від B до A— 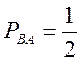 .
.
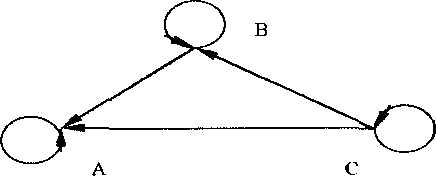
Мал. 1
Знайти матрицю перехідних імовірностей за два кроки.
Задача 10. Ланцюг Маркова описується матрицею 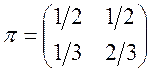 . Знайти фінальні імовірності.
. Знайти фінальні імовірності.
Задача 11.Випадкова функція ![]() задана вираженням
задана вираженням ![]() ,
, ![]() ,
, ![]() ,
, 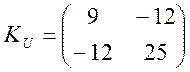 .
.
Привести дану випадкову функцію до канонічного виду.
Задача 12. Випадковий процес ![]() завдань наступним вираженням:
завдань наступним вираженням: ![]() , де
, де 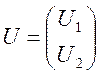 — випадковий вектор з вектором математичних
чекань
— випадковий вектор з вектором математичних
чекань 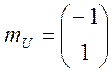 і коваріаціонною матрицею
і коваріаціонною матрицею 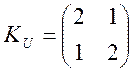 ; вектор координатних функцій
; вектор координатних функцій 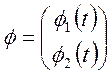 .
.
Знайти канонічне розкладання процесу ![]() і записати автоковариаційну функцію.
і записати автоковариаційну функцію.
Задача 13. Нехай ![]() випадковий процес,
випадковий процес, ![]() .
.
Знайти ![]() .
.
Задача 14. Нехай ![]() , де
, де ![]() і
і ![]() — випадкові величини.
— випадкові величини. ![]() ;
; ![]() ;
; 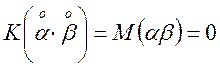 .
.
Знайти ![]() .
.
Задача 15. Випадковий процес ![]() , де
, де ![]() — випадкова величина така, що
— випадкова величина така, що ![]() . Знайти імовірні характеристики випадкового
процесу
. Знайти імовірні характеристики випадкового
процесу ![]() .
.
Задача 16. Задано випадковий процес ![]() , де
, де ![]() — дійсна невипадкова величина,
— дійсна невипадкова величина, ![]() — випадкова величина, де А — амплітуда,
— випадкова величина, де А — амплітуда,
![]() — зрушення по фазі, А і
— зрушення по фазі, А і ![]() незалежні випадкові величини,
незалежні випадкові величини, ![]() ,
, ![]() ,
, ![]() — рівномірний розподіл випадкової величини
на
— рівномірний розподіл випадкової величини
на ![]() , тобто
, тобто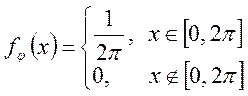 .
Знайти
.
Знайти ![]() .
.
Задача 17. Узагальнений телеграфний сигнал ![]() .
.
Імовірність зміни знака на інтервалі ![]() не залежить від того, що відбувалося поза цим інтервалом. Імовірність того, що протягом інтервалу тривалістю
не залежить від того, що відбувалося поза цим інтервалом. Імовірність того, що протягом інтервалу тривалістю ![]() відбудеться
відбудеться ![]() змін знака випадкової величини
змін знака випадкової величини ![]() :
:
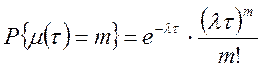 ,
, ![]() ,
,
![]() — середнє число змін значень випадкового процесу в одиницю години. Знайти імовірні характеристики узагальненого телеграфного сигналові й установити безперервність телеграфного сигналові.
— середнє число змін значень випадкового процесу в одиницю години. Знайти імовірні характеристики узагальненого телеграфного сигналові й установити безперервність телеграфного сигналові.
Задача 18.Випадкова
функція ![]() задана у виді
задана у виді ![]() , де
, де ![]() – випадкова величина, розподілена по
нормальному законі з параметрами
– випадкова величина, розподілена по
нормальному законі з параметрами ![]() ,
, ![]() ;
; ![]() – не
випадкова величина. Знайти одномірну щільність розподілу
– не
випадкова величина. Знайти одномірну щільність розподілу ![]() перетину випадкової функції
перетину випадкової функції ![]() і її характеристик:
і її характеристик: ![]() ,
, ![]() ,
, ![]() .
.
Задача 19.Дано характеристики нормального
випадкового процесу ![]() :
: ![]() ,
, ![]() ,
, ![]() .
Відомо, що в момент
.
Відомо, що в момент ![]() випадковий процес знаходиться в
стані
випадковий процес знаходиться в
стані ![]()
![]() . Знайти умовну
імовірність
. Знайти умовну
імовірність ![]() того, що в момент часу
того, що в момент часу ![]() випадковий процес
випадковий процес ![]() буде
належати деякої області
буде
належати деякої області ![]() :
:
![]() .
.
Задача 20.Задано випадкову функцію ![]() , де
, де ![]() і
і ![]() – некоррелированные випадкові величини з
характеристиками:
– некоррелированные випадкові величини з
характеристиками: ![]() ;
; ![]() ,
, ![]() . Знайти характеристики випадкової функції
. Знайти характеристики випадкової функції ![]() .
.
Задача 21.Розглядається лінійне перетворення ![]() випадкових процесів
випадкових процесів ![]() виду
виду 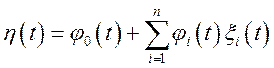 де
де ![]()
![]() – невипадкові функції
часу. Відомі характеристики випадкових процесів
– невипадкові функції
часу. Відомі характеристики випадкових процесів ![]() :
: ![]() ,
, ![]() ,
, ![]()
![]() , а також взаємні
кореляційні функції
, а також взаємні
кореляційні функції 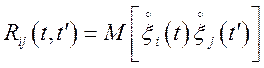
![]() .
Знайти характеристики випадкового процесу
.
Знайти характеристики випадкового процесу ![]() .
.
Задача 22.Знайти математичне чекання і
кореляційну функцію суми двох некоррелированных випадкових функцій ![]() і
і ![]() з
характеристиками:
з
характеристиками: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Задача 23.Комплексна випадкова функція ![]() задана у виді
задана у виді ![]() , де
, де
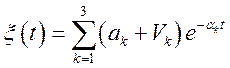 ;
; 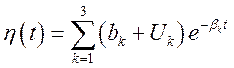 .
.
Математичні чекання усіх випадкових
величин ![]() і
і ![]()
![]() дорівнюють нулеві, а кореляційна матриця
системи випадкових величин
дорівнюють нулеві, а кореляційна матриця
системи випадкових величин ![]() має вигляд
має вигляд
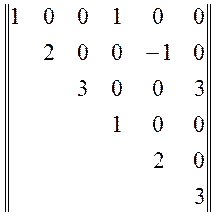
Знайти характеристики випадкової функції ![]() .
.
Задача 24.Кореляційна функція добутку. Розглядаються дві
некореліровані центровані випадкові функції ![]() ,
, ![]() і їхній добуток
і їхній добуток ![]() .
.
Довести, що кореляційна функція добутку дорівнює
добуткові кореляційних функцій співмножників: ![]() .
.
Задача 25.Випадкова функція ![]() має характеристики
має характеристики ![]() ;
;
![]() . Визначити характеристики випадкових
функцій
. Визначити характеристики випадкових
функцій
![]() ;
; 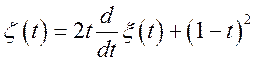 ;
; 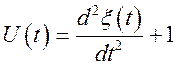 .
.
Задача 26.Характеристики інтеграла від
випадкового процесу. Мається випадковий процес ![]() і дані його
характеристики:
і дані його
характеристики: ![]() ,
, ![]() . Знайти
характеристики
. Знайти
характеристики ![]() ,
, ![]() інтеграла
цього випадкового процесу
інтеграла
цього випадкового процесу 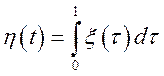 , а також взаємну
кореляційну функцію
, а також взаємну
кореляційну функцію ![]() .
.
Задача 27.Розглядається випадкова функція ![]() , де
, де ![]() —
центрована випадкова величина з дисперсією
—
центрована випадкова величина з дисперсією ![]() ;
; ![]() — випадкова величина, розподілена з
постійною щільністю в інтервалі
— випадкова величина, розподілена з
постійною щільністю в інтервалі ![]() , a
, a ![]() — невипадковий параметр
— невипадковий параметр ![]() . Випадкові величини
. Випадкові величини ![]() і
і ![]() незалежні.
Знайти характеристики випадкової функції
незалежні.
Знайти характеристики випадкової функції ![]() :
математичне чекання, кореляційну функцію. Визначити, чи є випадкова функція
:
математичне чекання, кореляційну функцію. Визначити, чи є випадкова функція ![]() стаціонарної і эргодической. Якщо вона
стационарна, то знайти її спектральну щільність
стаціонарної і эргодической. Якщо вона
стационарна, то знайти її спектральну щільність ![]() .
.
Задача 28.* Ознака позитивної визначеності.
Мається функція ![]() , що володіє властивостями: 1)
, що володіє властивостями: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
Потрібно з'ясувати, чи може функція ![]() бути кореляційною функцією стаціонарної
випадкової функції, тобто чи володіє вона властивістю позитивної визначеності.
Показати, що достатньою умовою позитивної визначеності є умова, щоб функція
бути кореляційною функцією стаціонарної
випадкової функції, тобто чи володіє вона властивістю позитивної визначеності.
Показати, що достатньою умовою позитивної визначеності є умова, щоб функція
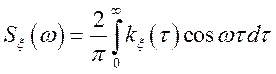 (*)
(*)
була ненегативна при будь-якому
значенні ![]() :
:
![]() (**)
(**)
т. е. щоб, обчислюючи спектральну щільність по формулі
(*), ми ні при яких ![]() не одержували негативних значень
цієї функції.
не одержували негативних значень
цієї функції.
Задача 29.* Визначити, чи володіє функція 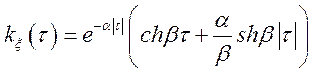
![]() властивостями
кореляційної функції.
властивостями
кореляційної функції.
Задача 30. Чи володіє функція 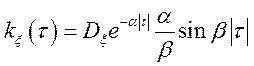 властивостями кореляційної функції?
властивостями кореляційної функції?
Задача 31.Випадкова функція ![]() має характеристики
має характеристики ![]() ;
;
![]() . Знайти її спектральну щільність.
. Знайти її спектральну щільність.
Задача 32.Випадкова функція ![]() задана власним канонічним розкладанням
задана власним канонічним розкладанням
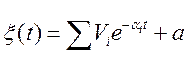 ,
,
де ![]() —
центровані випадкові величини з дисперсіями
—
центровані випадкові величини з дисперсіями ![]()
![]() ;
; ![]() при
при ![]() ;
; ![]() — не
випадкова величина. Знайти
— не
випадкова величина. Знайти ![]() ,
, ![]() ,
, ![]() .
.
Задача 33.Мається комплексна випадкова функція ![]() , де
, де ![]() — мнима
одиниця;
— мнима
одиниця; ![]() ,
, ![]() —
некореліровані випадкові функції з характеристиками
—
некореліровані випадкові функції з характеристиками
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Знайти характеристики випадкової функції ![]() :
: ![]() ,
, ![]() ,
, ![]() .
.
Задача 34.Розглядається випадковий процес 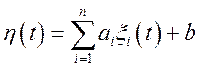 , де
, де ![]() —
стаціонарні некореліровані випадкові процеси з характеристиками:
—
стаціонарні некореліровані випадкові процеси з характеристиками: ![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() — дійсні числа. Знайти характеристики
випадкового процесу
— дійсні числа. Знайти характеристики
випадкового процесу ![]() .
.
Задача 35. Довести, що:
а) ![]() ;
;
б) 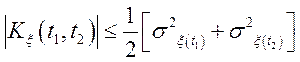 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.