Марковські процеси. Використання Марковських процесів для систем масового обслуговування

Лекція 12

План:

1.  Марковські процеси.

2. Використання Марковських процесів для систем масового обслуговування.

1.  Марковські процеси

Розглянемо  деяку фізичну систему , що протягом часу  і під впливом випадкових факторів переходить з одного стану в інше, тобто у фізичній системі  відбувається випадковий процес. Також допустимо, що існує, тільки кінцеве або кількість різних фазових, що перелічується, станів системи :

Позначимо  — стан системи в момент  .

Сукупність випадкових величин   називають випадковим процесом у  (еволюція системи).

Визначення.  Випадковий процес називають Марковським, якщо  послідовність  випадкових величин  є ланцюг Маркова, тобто

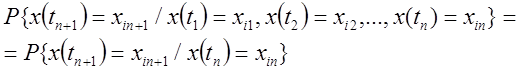             (12.1)

Визначення. Імовірністю переходу Марковського процесу буде функція , що задовольняє:

1)            

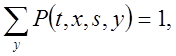
2) 

З визначення, ланцюга Маркова і формули (12.2) випливає,  теорема про спільні  розподіл Марковського процесу.

Теорема  1. Для

                 (12.2)

Теорема  2.

Рівняння Колмогорова — Чорніла:  

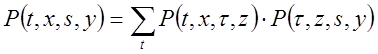                 (12.3)

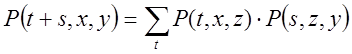                     (12.4)

–— для однорідних Марковських процесів.

Зручно формулу (12.4) записати в матричному виді, допускаючи, що множник станів  , збігається з множником усіх натуральних чисел   — імовірність переходу зі стану  в стан  за час   формула (12.4)  буде мати вигляд

           , ДЕ             (12.5)

(порядок  матриці збігається з  числами станів системи)

Визначення. Марковський процес називається стохастично-безперервним, якщо

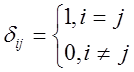 ,                     (12.6)

Визначення 4. Марковський процес називається локально регулярним, якщо він задовольняє  умовам:

1. У кожнім стані він проводить якийсь час, перед тим як вийти з нього

2. З кожного такого стану процес незалежно переходить у який-небудь інший

Теорема.  Для локально регулярного процесу існують границі

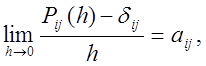                         (12.7)

при цьому  .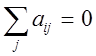

Зауваження. При доказі теореми одержимо дуже важливий висновок

                                            (12.8)

Це означає що час перебування в стані  “ ” показовий розподіл  з параметром . Якщо  стан  — поглинаюче: раз потрапляючи в цей стан, процес може з нього більше не залишити. Для  величина 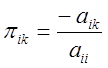 це імовірність того, що після виходу зі стану  процес безпосередньо попадає в стан .

Вентцель Е. С., Вівчарів Л.А. інтерпретує  як   цілісність потоку подій, що переводить систему зі стану  в стан .

Теорема. Якщо однорідний Марковський процес з перехідними імовірностями  локально регулярний, то виконується перша система рівнянь Колмогорова

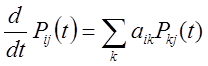                (12.9)

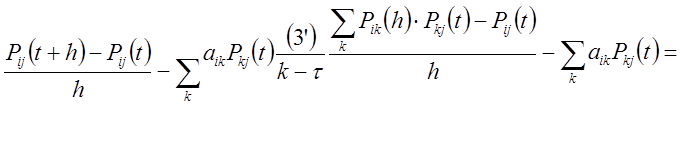
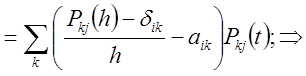 для ;

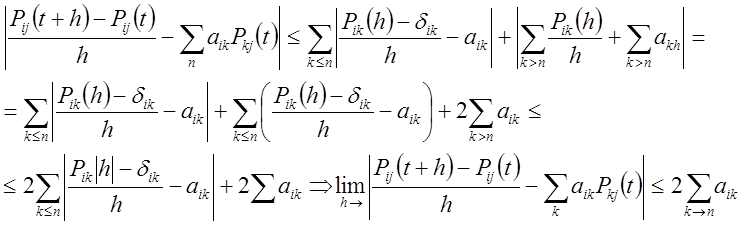
Отже, переходячи до границі при      одержимо (12.9). (12.9) — система звичайних диференціальних рівнянь з постійними коефіцієнтами. Початкова умова

.

Теорема. Нехай виконана умова

.

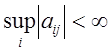Тоді  система рівнянь (12..9) має єдине рішення при початкових умовах  може бути записана  у виді

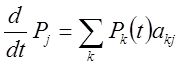                                  (12.10)

— інша пряма систем рівнянь Колмогорова; дає можливість  обчислювати  безумовні  розподіли процесів.

Вентцель Е.С., Вівчарів Л.А. для зручності додавання систем диференціальних рівнянь пропонують користуватися графом станів, на якому напроти кожної стрілки, що веде зі стану в стан проставлена щільність   потоку  подій, що переводить систему зі стану  в стан 

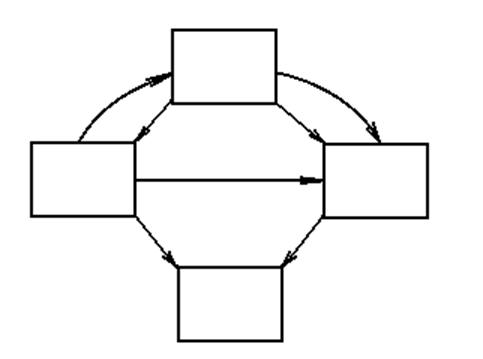
Якщо маємо такий граф  станів у системі , то систему диф. рівнянь відразу записати, користуючись наступним правилом. У лівій частині кожного рівняння коштує щільність 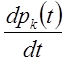, а в правій частині — стільки членів, скільки стрілок  пов'язано безпосередньо з даним станом; якщо стрілка веде в даний стан, член  має знак плюс, якщо веде з даного стану, то має знак мінус. Кожен член зрівнює добуту щільність потоку подій, що переводить  систему по довгій стрілці на імовірність того стану, з якого  виходить стрілка. Для системи , граф якої показаний на малюнку, система диф. рівнянь має вигляд

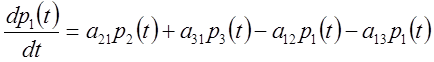
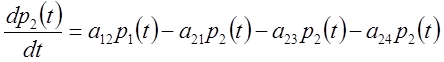
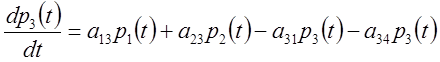
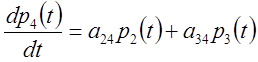
Число рівнянь  можна  замінити на функцію, якщо врахувати що

Початкові  умови відображають стан системи в початковий момент.