План:
1. Періодичний стаціонарний випадковий процес, спектральне розкладання цього процесу і його кореляційні функції.
1.1. Визначення і приклади.
1.2. Властивості періодичного випадкового процесу.
2. Неперіодичний стаціонарний процес і спектральне представлення його кореляційної функції.
3. Властивості спектральної щільності стаціонарного процесу.
Визначення. Стаціонарний випадковий процес називається періодичним
з періодом ![]() , якщо
, якщо ![]() .
.
Приклад.
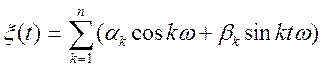 ,
,
де ![]() — невипадкова величина,
— невипадкова величина, ![]() і
і ![]() —
випадкові величини, при цьому
—
випадкові величини, при цьому ![]() , тобто центровані і
некоррелированные між собою.
, тобто центровані і
некоррелированные між собою.
![]() ,
, ![]() ;
;
![]() .
.
Рішення.
Перевіримо чи є процес періодичним.
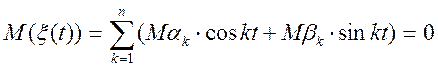 ,
,
отже, ![]() .
.
![]()
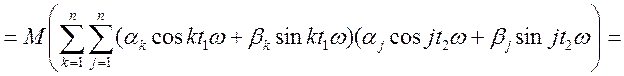
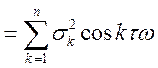 ,
, ![]() ,
,
т.е.
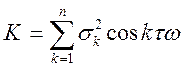 ,
,
отже, процес періодичний з періодом 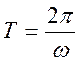 .
.
Приклад.
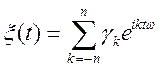 ,
,
де ![]() — невипадкова величина,
— невипадкова величина, ![]() ,
, ![]() ,
, ![]() .
.
Рішення.
Покажемо, що процес стаціонарний і періодичний.
![]() ;
;
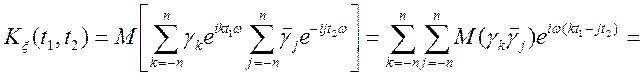
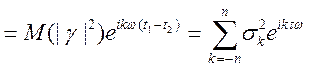 ,
, ![]() ,
,
процес стаціонарним і періодичний з періодом 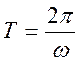 .
.
Приклад.
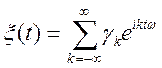 .
.
Показати, що ряд 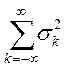 сходиться.
сходиться.
Рішення.
Якщо 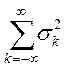 сходиться, то
сходиться, то 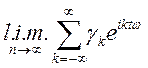 існує, це очевидно.
існує, це очевидно.
Нехай
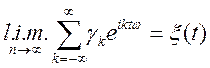 ,
,
тоді
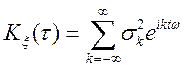 —
—
ряд сходиться абсолютно і період дорівнює 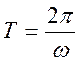 .
.
Періодичність випадкового процесу спричиняє періодичність його реалізацій і навпаки, якщо сума невипадкових гармоній представима для його кореляційних функцій, те і його реалізації так само періодичні.
Теорема. Якщо ![]() стаціонарний
періодичний процес з періодом
стаціонарний
періодичний процес з періодом ![]() , то його реалізації з
імовірністю рівній одиниці, є періодичними з тим же періодом. І навпаки, якщо
реалізації деякого стаціонарного процесу з імовірністю рівній одиниці є
періодичними функціями того самого періоду, те випадковий процес є періодичним
з тим же періодом (тобто його кореляційна функція має ту ж межу).
, то його реалізації з
імовірністю рівній одиниці, є періодичними з тим же періодом. І навпаки, якщо
реалізації деякого стаціонарного процесу з імовірністю рівній одиниці є
періодичними функціями того самого періоду, те випадковий процес є періодичним
з тим же періодом (тобто його кореляційна функція має ту ж межу).
(Без доказу).
Теорема. Якщо кореляційна функція —
періодична з періодом ![]() , то вона може бути представлена
за допомогою ряду Фур'є в комплексній формі:
, то вона може бути представлена
за допомогою ряду Фур'є в комплексній формі:
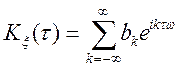 ,
, 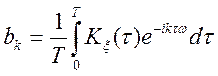 .
(9.1)
.
(9.1)
Питання в тім, чи можна аналогічно розкладанню періодичної функції на гармоніки, зробити відповідне розкладання випадкового періодичного процесу на суму випадкових гармонійних коливань?
Теорема. Якщо ![]() —
стаціонарний періодичний процес з періодом
—
стаціонарний періодичний процес з періодом ![]() , і його
кореляція
, і його
кореляція ![]() представима у виді ряду Фур'є (9.1), то
періодичний процес може бути представлений поруч виду
представима у виді ряду Фур'є (9.1), то
періодичний процес може бути представлений поруч виду
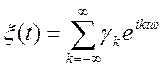 , (9.2)
, (9.2)
де 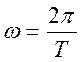 ,
, ![]() —
випадкова величина, що задовольняє умовам:
—
випадкова величина, що задовольняє умовам:
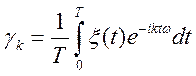 ,
,
![]() ,
, ![]() ,
, ![]() .
.
Визначення. Представлення випадкового процесу у виді (9.2) називається спектральним розкладанням процесу в комплексній формі.
Спектральне представлення зображує стаціонарний випадковий процес розкладеним на випадкові гармоніки різних частот:
![]() ,
, ![]() , …,
, …,![]() , …
, …
Загальний період ![]() .
.
Знайдемо дисперсію випадкового процесу, заданого своїм спектральним розкладанням.
Для стаціонарного випадкового процесу маємо:
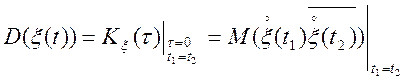 ,
,
т.к. 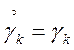
![]() , те
, те
![]() ,
,
отже,
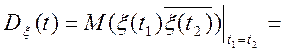
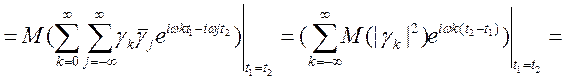
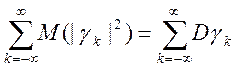 ,
,
т.е.
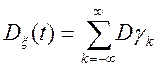 ,
,
отже, дисперсія стаціонарного випадкового процесу дорівнює сумі дисперсій усіх випадкових гармонік її спектрального розкладання. Графічно розподіл дисперсії по частотах можна представити так:
![]()
![]()
![]()
![]() Сума
ординат побудованого таким
Сума
ординат побудованого таким
![]() образом спектра дорівнює
дисперсії
образом спектра дорівнює
дисперсії
![]()
![]() випадкового
процесу
випадкового
процесу ![]() у випадку
у випадку
![]()
![]() збіжності
ряду
збіжності
ряду 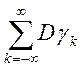 , тобто спектр стаціонарної випадкової
функції описує розподіл дисперсії по різних частотах.
, тобто спектр стаціонарної випадкової
функції описує розподіл дисперсії по різних частотах.
Якщо періодичний стаціонарний процес
представимо поруч Фур'є то за аналогією безперервний стаціонарний процес можна
представити інтегралом Фур'є на відрізку ![]() .
.
Спектральне представлення випадкового
періодичного процесу на кінцевому інтервалі ![]() :
:
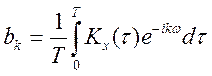 ,
, ![]() . (9.3)
. (9.3)
Якщо навіть поза інтервалом часу нам байдужна точність
опису процесу, то все рівно для безперервного випадкового процесу таке
представлення дає наближений опис. Більш повне представлення про випадковий
процес при його спектральному розкладанні може бути отримане при збільшенні
інтервалу ![]() (
(![]() ).
).
Теорема. (Хінчина) Кореляційна функція стаціонарного випадкового процесу з кінцевою дисперсією може бути представлена у виді
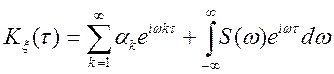 , (9.4)
, (9.4)
де ![]() — функція, що інтегрується,
називаною спектральною щільністю випадкового
— функція, що інтегрується,
називаною спектральною щільністю випадкового ![]() процесу
, при
процесу
, при ![]() цьому
цьому ![]()
![]() , .
, .
(Без доказу).
Якщо ввести в розгляд спектральну функцію
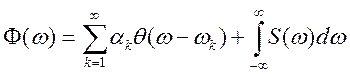 , (9.5)
, (9.5)
де 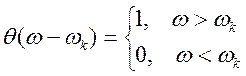 — одинична функція Хевисайда.
— одинична функція Хевисайда.
Тоді формула (9.4) для ![]() прикмет вид
прикмет вид
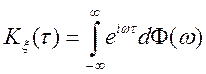 .
(9.6)
.
(9.6)
Для одержання цієї рівності використовується ![]() — функція Дирака
— функція Дирака 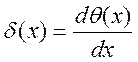 .
Її властивість
.
Її властивість 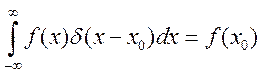 . Підставимо
. Підставимо ![]() (див.(9.5)) у вираження (9.6). Тоді
(див.(9.5)) у вираження (9.6). Тоді
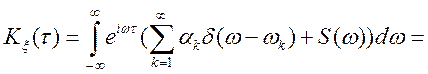
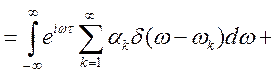
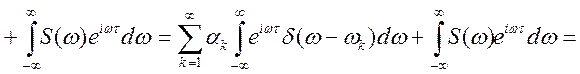
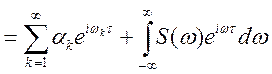 .
.
У такий спосіб равносильность (9.5) і (9.6) доведена.
З першої формули для спектральної функції випливає, що вона складається з двох доданків: перше — кусочно-постійна функція, друге — дифференцируемая функція (як інтеграл по верхній межі).
Розглянемо окремі окремі випадки.
1. ![]()
![]()
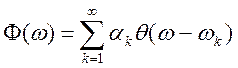 і
і 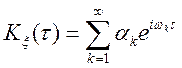 ,
,
у цьому випадку говорять, що випадковий процес має дискретний
спектр частот, а крапки ![]() називаються крапками
росту спектральної функції
називаються крапками
росту спектральної функції ![]() , що у цьому випадку
кусочно-постійна. У цьому випадку кореляційна функція не є інтегральною на
речовинній осі.
, що у цьому випадку
кусочно-постійна. У цьому випадку кореляційна функція не є інтегральною на
речовинній осі.
2. Якщо ![]()
![]() ,
тобто немає дискретних станів, то
,
тобто немає дискретних станів, то
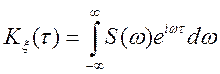 ,
, 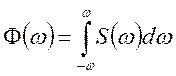 ,
,
отже спектральна функція ![]() —
диференційована, тобто
—
диференційована, тобто 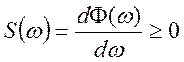 .
.
Т.о. установлений зв'язок між спектральною функцією і спектральною щільністю випадкового процесу.
Скориставшись зворотним перетворенням Фур'є, можна одержати вираження спектральної щільності через кореляційну функцію стаціонарного процесу:
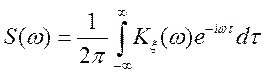 . (9.7)
. (9.7)
Цей окремий випадок приводить до випадкового процесу з безперервним спектром частот.
Для того, щоб кореляційна функція стаціонарного процесу могла бути представлена у виді інтеграла Фур'є, достатня її абсолютна интегрируемость:
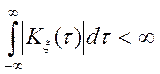 .
.
Властивість 1.
![]() .
.
Доказ.
На підставі вираження (9.7) і парності ![]() випливає
випливає
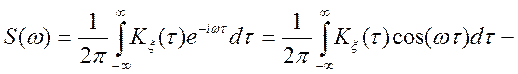
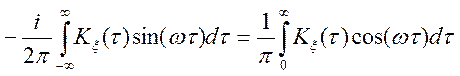 -
-
інтеграл від парної функції по параметрі ![]() , отже,
, отже, ![]() — парна
функція.
— парна
функція.
Властивість 2.
Якщо дисперсія ![]() ,
, ![]() , — обмежена величина, то
, — обмежена величина, то ![]() — функція, що інтегрується, тобто
— функція, що інтегрується, тобто 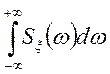 — сходиться.
— сходиться.
Доказ.
Покладемо ![]() в
в 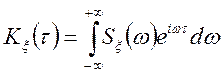 , отже,
, отже,
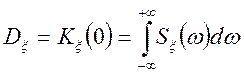 ,
,
але ![]() — скінченний величина, значить
— скінченний величина, значить 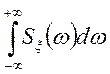 дорівнює кінцевому числу, тобто
дорівнює кінцевому числу, тобто ![]() сходиться.
сходиться.
Властивість 3.
![]() .
.
Доказ.
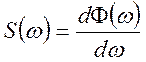 ,
,
але ![]() неубутна функція.
неубутна функція.
Приклад.
Дана
![]() ;
;
Знайти ![]() .
.
Рішення.
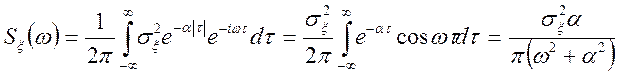 ;
;
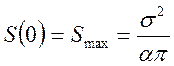 .
.
Якщо ![]() , то
, то ![]() , те
, те 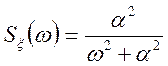 .
.
Визначення. Білим шумом називається випадковий процес з
постійною спектральною щільністю для всіх частот від ![]() ,
до
,
до ![]() .
.
Отже, для «білого шуму» характерно рівномірний
розподіл енергії випадкового процесу по всіх частотах. Реально такого процесу
немає (не існує), але це поняття є зручною асоціацією, коли ![]() близько до постійної величини
близько до постійної величини
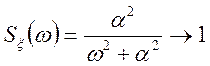 при
при ![]() .
.
Приклад.
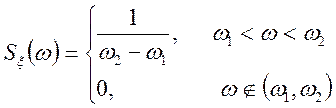 .
.
Знайти ![]() .
.
Рішення.
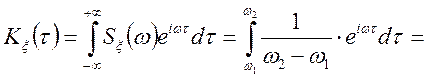
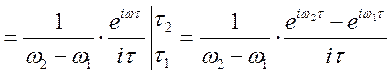 .
.
Якщо інтервал ![]() симетричний,
симетричний,
![]() , то
, то
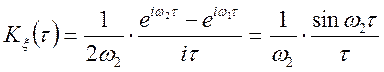 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.