Пошук характеристик випадкового процесу. Кореляційна функція добутку. Імпульсний дробовий ефект

Лабораторне заняття № 2

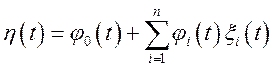Задача 1. Розглядається лінійне перетворення  випадкових процесів  виду  де  — невипадкові функції часу.

Відомі характеристики випадкових процесів : , ,  , а також взаємні кореляційні функції 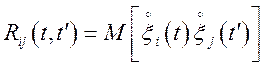 . Знайти характеристики випадкового процесу .

Рішення. ;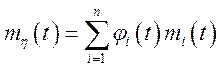

;

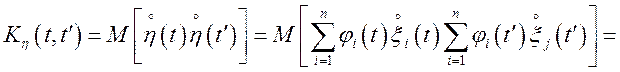
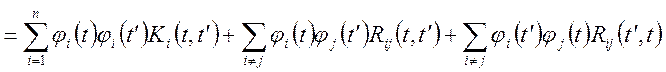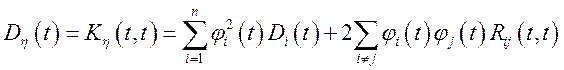
Якщо випадкові процеси   некореліровані ( ; ), то ; .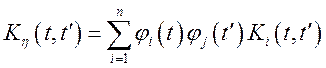

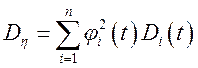Задача 2. Кореляційна функція добутку. Розглядаються дві некореліровані центровані випадкові функції ,  і їхній добуток .

Довести, що кореляційна функція добутку дорівнює добуткові кореляційних функцій співмножників: .

Рішення. 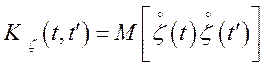; 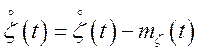. Тому що випадкові функції ,  некореліровані і центровані, те ; звідси ;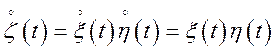

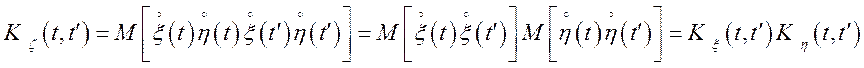
Зокрема, при  .

 Задача 3.  Імпульсний дробовий ефект. Розглядається дробовий ефект, породжуваний імпульсами, що мають прямокутну форму; при цьому амплітуда  і тривалість  імпульсу, що надходить у момент  – незалежні випадкові величини з характеристиками ; ;  і  і відповідно (мал. 1). Знайти математичне чекання і дисперсію такого випадкового процесу .

Рішення. Розглянутий імпульсний дробовий ефект на ділянці  можна представити у виді 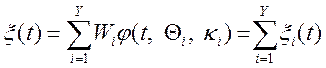, де  — імпульс, початок якого приходиться на момент часу , висота дорівнює одиниці, а тривалість  (випадкові величини  і  — незалежні): . Випадкова величина  розподілена рівномірно усередині інтервалу .

Знайдемо . Уведемо гіпотезу, що складається в тім, що випадкова величина  прийняла значення . У пропозиції, що ця гіпотеза мала місце, знайдемо умовне математичне чекання при досить великих значеннях :

.

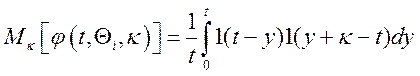Подынтегральная функція являє собою прямокутний імпульс з висотою, рівній одиниці, і тривалістю, рівної , а інтеграл від цієї функції буде дорівнює площі цього імпульсу. Отже,

,

Відкіля

.

Аналогічно

;

.

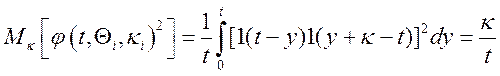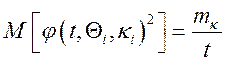Отже, ;

; ; .

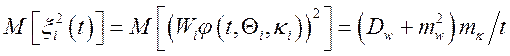У межі при необмеженому збільшенні інтенсивності найпростішого потоку , дисперсії амплітуди імпульсу , необмеженому зменшенні математичного чекання  і дисперсії  тривалість імпульсу і збереженні постійної величини , тоді імпульсний дробовий ефект перетворюється в білий шум з характеристиками ; .