Спектральне розкладання стаціонарних випадкових функцій. Лінійний фільтр

Лекція 10

План:

1. Спектральне розкладання стаціонарних випадкових функцій.

2. Лінійний фільтр.

1.  Спектральне розкладання стаціонарних випадкових функцій

Визначення. Стаціонарна в широкому змісті випадкова функція , задана у всій області визначення параметра , що задається канонічним розкладанням виду

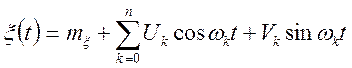,                   (10.1)

де  і  — центровані випадкові величини, що задовольняють умовам

; , ,

називається випадковою функцією з дискретним спектром.

Визначення. Якщо  — час, то випадковий процес задава формулою (10.1) називається випадковий процес з дискретним спектром.

Автоковариационная функція такого процесу має такий вид

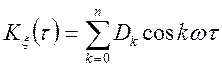,                            (10.2)

Визначення. Представлення (10.1) і (10.2) називаються спектральним розкладанням випадкового процесу, випадкової функції.

Дисперсія випадкової функції з дискретним спектром має вигляд:

.

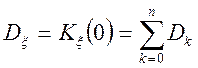У випадку, якщо , а 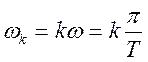, те формули (10.1) і (10.2) дають наш ряд Фур'є, причому  — парна функція.

Стаціонарні випадкові функції розглянуті на кожнім проміжку  завжди можуть бути представлені у виді спектральних розкладань (10.1) і (10.2). Якщо кореляційна функція  не є періодичної, то стаціонарний випадковий процес  не може бути представлений на всій осі  представленнями у виді (10.1) і (10.2) і, отже, не є при всіх дійсних  процесом з дискретним спектром.

Стаціонарна випадкова функція  називається випадковою функцією з безперервним спектром, якщо існує дійсна ненегативна функція  визначена на всій осі частот  в інтервалі  і називається спектральною щільністю, що справедливі наступні інтегральні формули (інтегральні формули Видера-Хинчина)

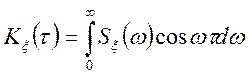               (10.3)

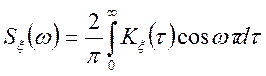              (10.4)

Для їхньої справедливості досить, щоб ковариационная функція  була дифференцируема на . У такий спосіб кореляційна функція і спектральна щільність стаціонарної випадкової функції з безперервним спектром зв'язані один з одним взаємно зворотними косинусами-перетвореннями Фур'є. З (10.3), (10.4) і властивостей кореляційної функції випливає, що  — парна функція.

У силу парності подынтегральных функцій у формулах Винера-Хинчина (10.3), (10.4) останні можуть бути записані в експонентному виді

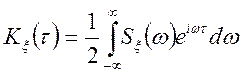                (10.5)

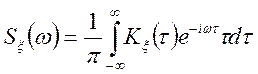               (10.6)

З цих формул випливає, що дисперсія може бути виражена у виді інтеграла від спектральної щільності

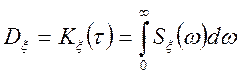
Умови ,  для  є необхідною умовою стаціонарності в широкому змісті стаціонарної випадкової функції .

Корисними характеристиками стаціонарних випадкових функцій з безперервним спектром є:

-  ефективна ширина спектра ;

-  середній інтервал кореляції  (ефективна тривалість кореляційної функції)

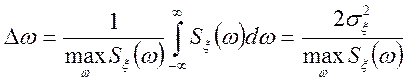                  (10.7)

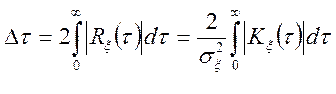                    (10.8)

.

2.   Лінійний фільтр

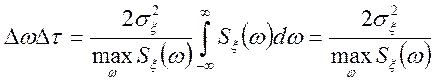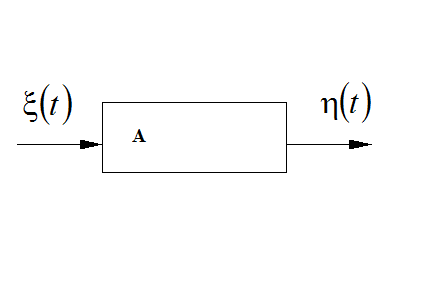
Система  здійснює над цим випадковим процесом .

Всі операції такого виду  можна розбити на двох груп:          

1) лінійні:

-  однорідні;

-  неоднорідні

2) нелінійні.

Лінійність — це наступна властивість: якщо на вхід системи надходить суміш сигналів, те її обробка еквівалентна тому, як якби ми зміщали результати обробки кожного сигналу окремо.

Визначення.Оператор  називається лінійні й однорідним, якщо виконуються умови:

1. ;

2. .

Очевидно, що операції диференціювання й інтегрування відносяться до лінійним однорідного.

Нехай на вхід лінійної динамічної системи з постійними параметрами (така система називається стаціонарною лінійною системою) надходить стаціонарний випадковий процес, характеристики якого відомі. Потрібно визначити характеристики випадкового процесу на виході.

У загальному випадку, робота лінійної динамічної системи з постійними параметрами описується диференціальним рівнянням виду:

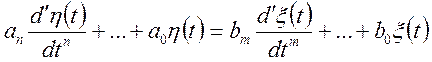         (10.9)

Залежність між  і  будемо називати лінійним однорідним оператором.

Якщо , то інтегральний оператор .

Якщо , то диференціальний оператор .

Якщо  досить вилучено від початку процесу, усі перехідні процеси в системі можна вважати закінченими процесами і система працює у встановленому режимі.