Індивідуальне завдання № 20
Задача 1.Випадкова функція 
,де 
і 
—незалежні ВВ,
що підкоряються
тому самому нормальному законові розподілу 
. Використовуючи властивості математичного чекання
і дисперсії обчислити 
, 
, 
і одномірну щільність 
.
Задача 2. Довести, що кореляційна функція не змінюється від додавання до випадкової функції будь-якої невипадкової функції.
Задача 3. Швидкість літака визначається гіроскопічним інтегратором, що дає помилку
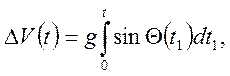
де 
—
помилка стабілізації осі інтегратора, що має кореляційну функцію
радий2=
,
а 
— прискорення
сили ваги. Знайти середню квадратическую помилку визначення швидкості після 10
годин польоту (
дане в сек.).
Задача 4.Випадковий процес заданий у виді 
, де — ВB з 
, 
.
Знайти імовірностні характеристики
випадкового процесу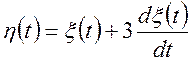 
.
Задача 5. Нехай даний випадковий вектор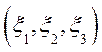 
з
математичним чеканням (0, 0, 0) і кореляційною матрицею
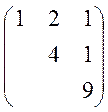
Чи можна його лінійним перетворенням простору привести до вектора з попарно некорелірованими компонентами?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
