Векторний випадковий процес. Комплексний випадковий процес

Лекція  4

План:

1. Векторний випадковий процес.

1.1. Визначення векторного випадкового процесу. Кореляційна  матриця.

1.2. Властивості кореляційної функції векторного процесу.

2. Комплексний випадковий процес.

1.   Векторний випадковий процес

1.1. Визначення векторного випадкового процесу. Кореляційна матриця

Набір випадкових процесів  можна інтерпретувати як вектор , компоненти якого є випадкові процеси, і записувати у виді

.                             (4.1)

Характеристики векторного процесу також є векторами

                   (4.2)

,                   (4.3)

де  — математичне чекання векторного випадкового процесу, а — математичне чекання -ой компонента. Аналогічно і для дисперсії.

Інформацію про зв'язок між компонентами векторного випадкового процесу несе кореляційна матриця , кожен елемент якої — функція двох перемінних  і

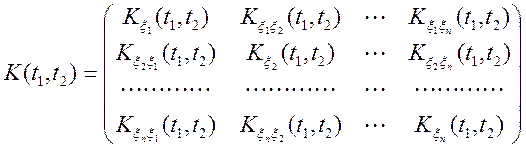,            (4.4)

де

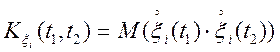 —                        (4.5)

кореляційна функція випадкового процесу , а

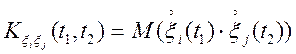 —                             (4.6)

взаємна кореляційна функція між двома випадковими процесами  і . У загальному випадку матриця не є симетричної, тому що

.

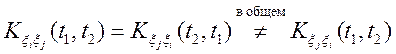Розглянемо двовимірний векторний випадковий процес , тобто . Тоді маємо

,                                 (4.7)

,                                 (4.8)

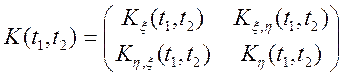,                 (4.9)

де

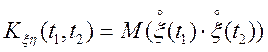.                 (4.10)

(4.10) — взаємна кореляційна функція двох процесів і .

Якщо задано щільність  спільного розподілу випадкової величини  і  при фіксованих , то  являє собою кореляційний момент, а саме

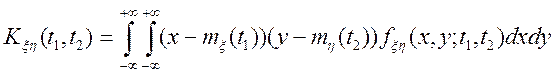.   (4.11)

1.2.    Властивості кореляційної функції векторного процесу

Властивість  1.

                                     (4.12)

Доказ.

У рівності (4.10) покладемо , тоді

.

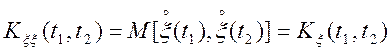Визначення. Якщо взаємно кореляційна функція двох випадкових процесів  дорівнює нулеві для будь-яких , тобто

, ,                                     (4.13)

те випадкові процеси  і  називаються некорелірованими.

Властивість  2.

  (4.14)

Доказ.

Спочатку покажемо, що

                                  (4.15)

.

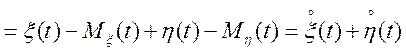Далі, використовуючи формулу (4.10) і властивості математичного чекання, одержуємо

.

Що і було потрібно довести.

Властивість 3.

Якщо випадкові процеси  і  некореліровані, то кореляційна функція їхньої суми дорівнює сумі кореляційних функцій

.            (4.16)

Використовуючи визначення некоррелированных двох випадкових процесів (4.13), одержимо (4.16) з (4.14).

Наслідок. Для некорелірованих випадкових процесів дисперсія суми дорівнює сумі дисперсій, тобто якщо , те

                             (4.17)

З властивості 1 кореляційної функції випадкового процесу  і (4.16), одержуємо

.

2.   Комплексний випадковий процес

          Комплексні випадкові процеси в основному зустрічаються в задачах радіотехніки, узагалі зв'язані з хвильовими процесами

,

по визначенню

.

Властивості:

1)   

Доказ.

.

2)   

.

Доказ.

.

Визначення. Кореляційна функція комплексного випадкового процесу має вигляд:

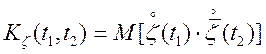.                (4.18)

Можна довести, що

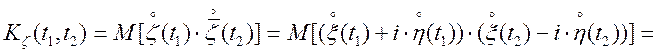
.            (4.19)

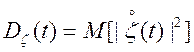.                        (4.20)

З (4.18) випливає . Дійсно, 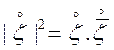, тоді, згідно (4.20),

.

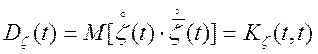З (4.19) випливає  

.

Т.о. .

Приклад.

,  — дійсна невипадкова величина,

, де  — амплітуда,  — зрушення по фазі,  і  незалежні випадкові величини, , ,  — рівномірний розподіл випадкової величини на , тобто .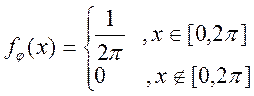

Знайти , , .

Рішення.

Т.к.  і  — незалежні, те

3.  .

 

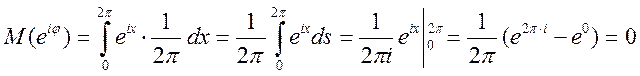
Т.о. .

4.  .

,

   ,

   ,

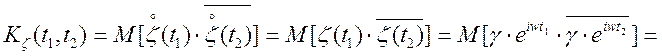
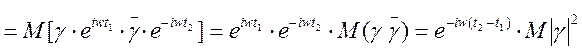5.   .