Спектральне розкладання стаціонарних випадкових функцій. Лінійний фільтр, страница 2

Якщо на вході стаціонарний процес, то і на виході — стаціонарний. Нехай у рівнянні (10.9) , де  — стаціонарний процес з математичним чеканням  і кореляційною функцією . Знайти зв'язок між спектральною щільністю  і .

Насамперед відомі:

; ,

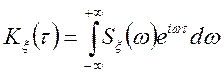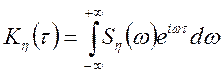продифференцируем двічі по параметрі , припускаючи його рівномірну збіжність.

З іншої сторони .

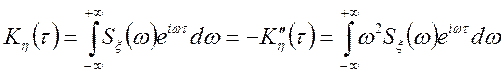;   (10.10)

                      (10.11)

Розглянемо лінійний диференціальний оператор виду

              (10.12)

Або в більш компактній формі

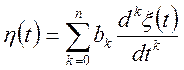                   (10.13)

Потрібно встановити зв'язок між спектральною щільністю при  на виході динамічної системи.

Нехай кореляційна функція процесу  задана у виді .

Очевидно, що  є лінійною й однорідної, те

                       (10.14)

       (10.15)

Якщо ж процес комплексний, то

,

де — комплексно сполучена перемінна.

Якщо записати через

,                              (10.16)

де

Для випадку (10.12) ми маємо

.

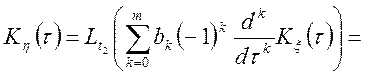
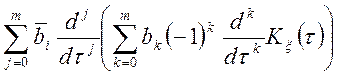Допустимо, що  така, що інтеграл 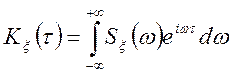 можна диференціювати по , тоді одержимо

.

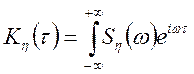
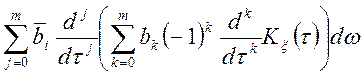Якщо позначити

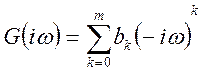,                        (10.17)

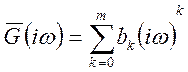,                         (10.18)

,

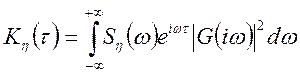,                        (10.19)

,                                 (10.20)

Функцію  називають частотною характеристикою оператора.

Самий загальний випадок

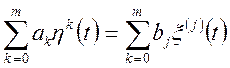,                                 (10.21)

це формула (10.9) у загальному виді. Те можна показати, що

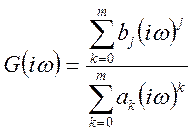,                       (10.22)

що частотна характеристика загального лінійного фільтра.

Приклад. Нехай динамічна система описується рівнянням

 

, .

Визначити .

Рішення.

; ;

.

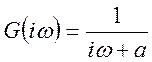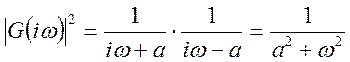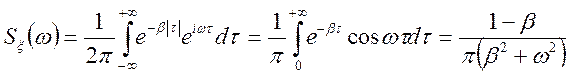
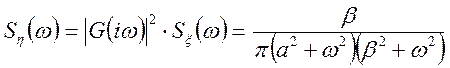
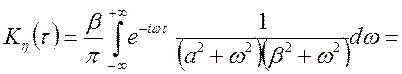
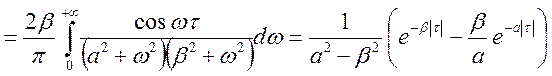Перетворення стаціонарної випадкової функції лінійними динамічними системами з постійними коефіцієнтами.

Лінійною динамічною системою з постійними коефіцієнтами називається система

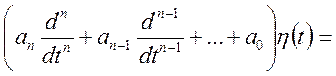
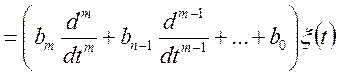,        (10.23)

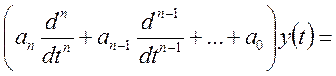
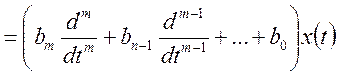,         (10.24)

де   — реалізація вхідного випадкового стаціонарного процесу;

       — реалізація процесу на виході системи.

Рівняння (10.23) описує зв'язок між випадковими функціями на вході і виході системи, а рівняння (10.24) описує зв'язок між реалізаціями вхідного випадкового процесу  і  — реалізації процесу на виході.

Визначення. Передатною функцією лінійної динамічної системи називається функція комплексного перемінного , визначена

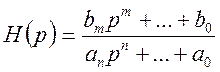.                            (10.25)

Функція  — є відношення перетвореним по Лапласу вихідного сигналу до вхідного сигналу, обумовлених з рівняння (10.24) при нульових початкових умовах. Властивості сигналу на виході цілком визначаються властивостями передатної функції  і властивостями вхідного сигналу. Говорять, що лінійна динамічна система задовольняє умові стійкості, якщо  не має полюсів у першій напівплощині комплексної площини  ( ).

Якщо на вхід стійкої лінійної динамічної системи з постійними коефіцієнтами подається стаціонарний вхідний сигнал, то по події досить великого часу з моменту початку впливу ( , де  — характерний час релаксації перехідних процесів) сигнал на виході системи буде близький до стаціонарного в широкому змісті процесові.

Якщо  — вхідний стаціонарний сигнал з характеристиками  і , у стаціонарному режимі ( )

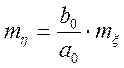                         (10.26)

                               (10.27)

Функція  називається амплітудно-частотною характеристикою системи.

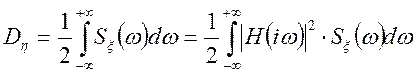(10.28)

Для кінцівки дисперсії необхідно і досить збіжність невласного інтеграла в (10.27). Достатнім, наприклад, є умова, щоб порядок оператора диференціального оператора вхідного сигналу у формулі (10.24) був не вище порядку диференціювання оператора вхідного сигналу ( ).

Приклад.

, ,  

Визначити:

а) , стійкість;

б) , ,  — на виході.

Рішення.

а) , ;  — умови стійкості виконаються.

; ; ; .

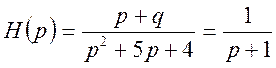Отже, умова стійкості виконана.

б)

.

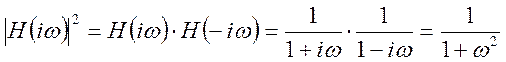Для процесу з ,

.

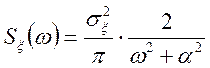Знаходимо по формулах (10.25)

.

.

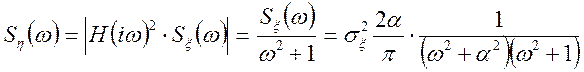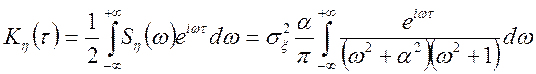Останній інтеграл знаходимо по відрахуваннях у верхній напівплощині

.

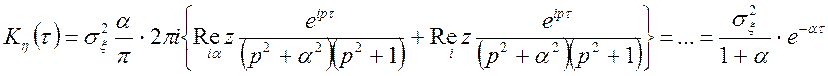У силу парності маємо в  раз менше дисперсії на вході. Це порозумівається тим, що дана динамічна система власне кажучи є інтегруючою метою, а операція інтегрування процесу згладжує шум.