Пошук одномірної функції і щільністі розподілу. Пошук спектральної щільністі функції

Лабораторне заняття № 5

Задача 1. Випадковий процес має вигляд ВВ, рівномірно розподілена на відрізку . Знайти одномірну функцію і щільність розподілу.

Рішення. По визначенню =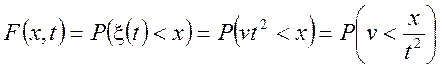

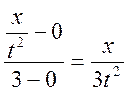. Тоді .

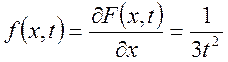Задача 2. Випадкова функція  має характеристики ; . Знайти її спектральну щільність.

Рішення. ,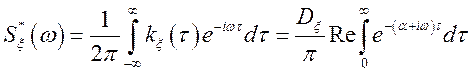

де Re – дійсна частина. Маємо

;

.

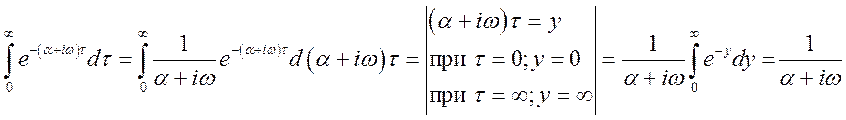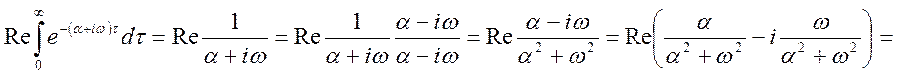
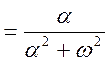Отже, .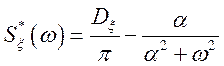

Задача 3. * Ознака позитивної визначеності. Мається функція , що володіє властивостями: 1) ; 2) ; 3) .

Потрібно з'ясувати, чи може функція  бути кореляційною функцією стаціонарної випадкової функції, тобто чи володіє вона властивістю позитивної визначеності. Показати, що достатньою умовою позитивної визначеності є умова, щоб функція

                                                    (*)

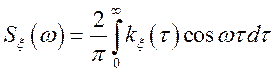була ненегативна при будь-якому значенні :

                                                         (**)

т. е. щоб, обчислюючи спектральну щільність по формулі (*), ми ні при яких  не одержували негативних значень цієї функції.

Рішення. Припустимо, що , і доведемо, що при цьому функція  буде позитивно визначеною. Маємо

           (***)

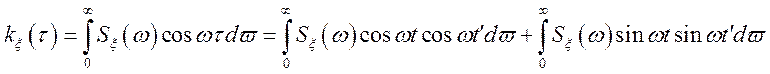Позитивна визначеність функції  полягає в тому, що для будь-якої функції  і будь-якої області інтегрування (У) повинне виконуватися умову

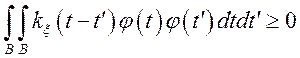
Перевіримо цю нерівність стосовно функції (***);

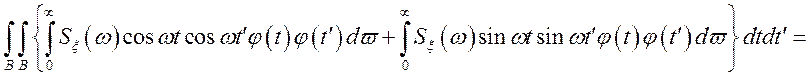
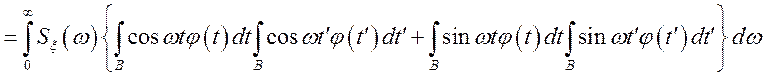
Позначаючи ; ,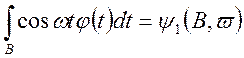

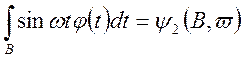одержуємо ,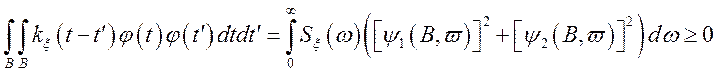

тому що за умовою .

Можна довести, що умова (***) є не тільки достатнім, але і необхідним для того, щоб кореляційна функція була позитивно визначеною.

Задача 4. На осі  мається найпростіший (стаціонарний пуасоновський) потік подій з інтенсивністю . Випадковий процес виникає в такий спосіб: у момент появи i-го події в потоці  він приймає випадкове значення  і зберігає його до наступної події в потоці . У початковий момент . Випадкові величини , , , …, , незалежні і мають те саме розподіл із щільністю . Знайти характеристики процесу , , .  Чи є процес стаціонарним?

Рішення. Будь-який перетин випадкової функції розподілено за законом ; звідси  ;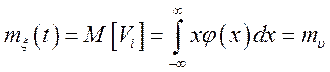

;

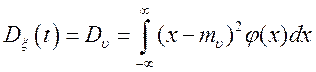Для перебування кореляційної функції , розглянемо два перетини і  , розділені інтервалом . Маємо

.

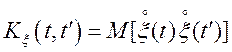Якщо між крапками ,  не з'явилося жодного події, то  і 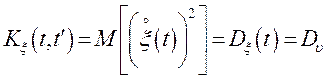. Якщо між крапками ,  з'явилося хоча б одна подія, то . Звідси

.

Аналогічно при

,

відкіля видно, що процес стаціонарен. Його кореляційна функція  не залежить від виду закону розподілу , а залежить тільки від його дисперсії .