Моментні функції. Кореліровані і некореліровані випадкові процеси

Лекція 3

План:

1. Моментні функції.

2. Кореліровані і некореліровані випадкові процеси.

1.  Моментні функції

Вичерпні характеристики випадкової функції в широкому змісті дає сімейство спільних розподілів. Однак у багатьох випадках становить інтерес більш стиснута характеристика розподілу, що відбиває деякої властивості випадкової функції. Крім того, рішення багатьох теоретико-вероятностных задач залежить тільки від невеликого числа параметрів, що характеризують вхідні в задачу розподілу. Найбільш важливими характеристиками рішень є їхні моменти. У теорії випадкових функцій роль моментів розподілу грають моментные функції.

Визначення. Моментными функціями

  випадкової функції  називаються функції

,   (3.1)

якщо математичне чекання в першій частині рівності має сенс при усіх  Величина  називається порядком моменту функції.

Визначення. Випадкова величина  належить класові , якщо  для кожного .

Теорема. Якщо , то моментные функції порядку  кінцеві для усіх  ( див. Гихман стор.17 ).

Якщо відомо характеристичну функцію спільного розподілу величин

,

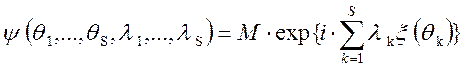те моментные функції з целочисленными індексами можуть бути знайдені за допомогою диференціювання. Дійсно,

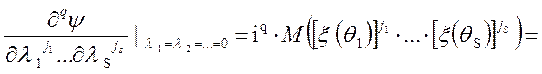
 —     (3.2)

узагальнення характеристичної функції на випадок будь-якого випадкового процесу. Випадкова функція породжує випадковий вектор довільної розмірності, у даному випадку не більш , причому диференціювання під знаком математичного чекання, у всякому разі законно для усіх 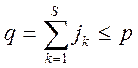, якщо  Точне звертання цього твердження мається тільки для  моментів функцій з парними індексами (див. Гихман стор.18,19,20).

Теорема.  Якщо характеристична функція - раз дифференцируема (p — парне), то існують моменти функції порядку  і вони можуть бути обчислені по формулі (2).

Крім моментів функцій, часто розглядаються центральні моменти функції:

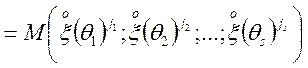,      (3.3)

які є  моментными функціями центрованої випадкової функції , що має при будь-якому  математичне чекання, рівне 0.

Серед моментных функцій особливе значення мають функції перших двох порядків  

                             (3.4)

     (3.5)

Функція  називається середнім значенням, а  — кореляційною функцією. При  кореляційна функція дає дисперсію  величини , . Для стаціонарного процесу, мабуть, що

                          (3.6)

                        (3.7)

Функція  також називається кореляційною функцією стаціонарного процесу. Якщо для деякого процесу виконуються рівності (3.6) і (3.7), то звідси ще не випливає, що процес стаціонарний. 

Частіше зустрічаються задачі, рішення яких залежить тільки від моментів перших двох порядків с.ф. . Для даних задач умова стаціонарності процесу зводиться до умов (3.6) і (3.7). Тому природно розглянути клас процесів, уведених Хинчиным А. Я. У рамках кореляційної теорії.

Визначення. Випадковий процес  називається стаціонарної в широкому змісті, якщо:

1) ;

2)  не залежить від часу;

3) другий змішаний центрований момент — функція, що залежить тільки від різниці:

Для стаціонарного в широкому змісті процесу дисперсія  випадкової величини  не залежить від .

2.   Кореліровані і некореліровані випадкові процеси

Визначення. Величина

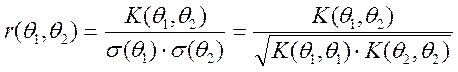
називається коефіцієнтом кореляції випадкових функцій  і .

Якщо  і  незалежні, то коефіцієнт кореляції дорівнює нулеві. Зворотне, узагалі говорячи, невірно. Все-таки у важливому окремому випадку, коли випадкові величини  і  мають спільний нормальний розподіл

,

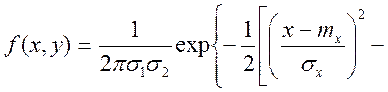
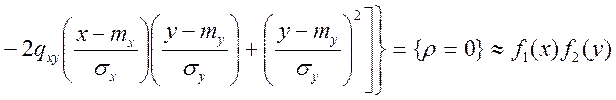 з рівності нулеві коефіцієнта кореляції або, що теж саме, кореляційної функції  випливає, що величини  і  незалежні. У загальному випадку дві випадкові величини  і  з кінцевими моментами другого порядку, що задовольняють умові

,

 називаються некоррелированными.

У тих розділах теорії, що зв'язані тільки з моментами першого і другого порядків, узагалі поняття некоррелированности заміняє поняття незалежності. Що ж стосується коефіцієнта кореляції пари випадкових величин, то він є мірою лінійного зв'язку між ними, тобто коефіцієнт кореляції показує, з якою точністю одна випадкова величина може бути лінійно виражена через іншу. Т.е. перевіркою незалежності будемо вважати рівність .

Приймемо за міру погрішності  наближеної рівності , де  і  постійні числа, величину . Тоді

.

.

.

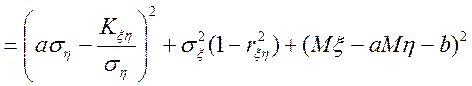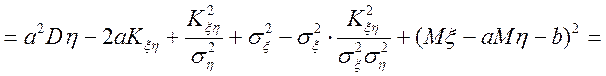
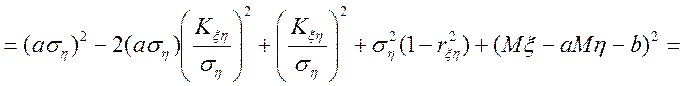
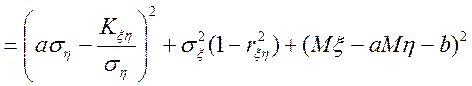Це вираження досягає мінімуму при

  ,

,

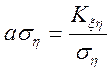
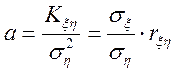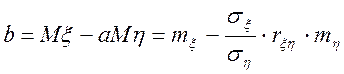 і його мінімальне значення дорівнює

.

Таким чином, чим більше по абсолютній величині , з тим більшою точністю одна з них може бути виражена у виді лінійної функції від іншої, причому коефіцієнти лінійної регресії отримані в явному виді.