Наприклад, якщо система в початковий момент ![]() , могла
, могла ![]() , те
, те
![]()
![]() при
при ![]() .
.
Якщо всі потоки стаціонарні ![]() ,
то існує кінцевий режим, що характеризується, імовірностями
,
то існує кінцевий режим, що характеризується, імовірностями 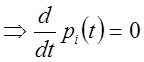 і система (8) має вигляд лінійного
алгебраїчного рівняння.
і система (8) має вигляд лінійного
алгебраїчного рівняння.
![]() (12.11)
(12.11)
2. Використання теорії Марковських процесів для систем масового обслуговування.
Системою масового обслуговування називається будь-яка система, що призначена, для обслуговування якогось потоку заявок (на приклад ремонтна майстерня, телефонна станція, квиткова каса і т.п.)
Системи масового обслуговування підрозділяються, на системи з відмовленнями і системи з чеканням.
У системі з відмовленнями заявка, що прийшла в той момент, коли всі канали обслуговування зайняті, одержує відмовлення і залишає систему.
У системі з чеканням, така заявка, не залишає
систему, а стає в чергу й очікує поки не звільниться який ні будь канал. Час
чекання і число місць у черзі можуть бути як нескінченними ![]() , так і обмеженими
, так і обмеженими ![]() .
.
Можна показати, що в будь-якому випадку процес, що
характеризує систему в момент ![]() буде однорідним
Марковським. Якщо
буде однорідним
Марковським. Якщо ![]() — час обслуговування якоїсь
заявки, то воно має показовий розподіл з параметром
— час обслуговування якоїсь
заявки, то воно має показовий розподіл з параметром ![]()
![]() (12.12)
(12.12)
нехай у момент ![]() у системі було
у системі було ![]() заявок. Якщо серед них обслуговується
заявок. Якщо серед них обслуговується ![]() , то час до закінчення обслуговування
кожної заявки не залежить від часу їхнього надходження і має показовий розподіл
таке точно як
, то час до закінчення обслуговування
кожної заявки не залежить від часу їхнього надходження і має показовий розподіл
таке точно як ![]() . Далі, час до приходу чергової
заявки не залежить від того, як давно прийшла попередня заявка.
. Далі, час до приходу чергової
заявки не залежить від того, як давно прийшла попередня заявка.
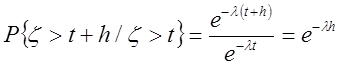 .
.
Одержимо для марковського процесу, що описує систему масового обслуговування, систему диференціальних рівнянь Колмогорова.
Робота СМО з відмовленнями визначається наступними параметрами
1. Число каналів ![]() .
.
2. Щільність потоку заявок ![]() (параметр
показового розподілу послідовності
(параметр
показового розподілу послідовності ![]() , де
, де ![]() час приходу чергової заявки
час приходу чергової заявки ![]() .
.
3. Щільність потоку обслуговування одного каналу ![]() .
.
![]() ,
, ![]() — час обслуговування заявки.
— час обслуговування заявки.
Зауваження. 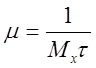 , тобто величина
середнього часу обслуговування.
, тобто величина
середнього часу обслуговування.
На мал.2 показаний граф станів ![]() -канального
СМО з відмовленнями. Стан
-канального
СМО з відмовленнями. Стан ![]()
![]() таке, що зайнято рівно
таке, що зайнято рівно ![]() каналів з
каналів з ![]() . З
цього графа випливають диференціальні рівняння для імовірності станів.
. З
цього графа випливають диференціальні рівняння для імовірності станів.
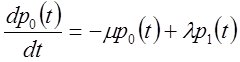
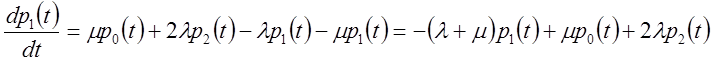
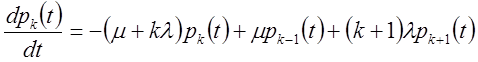
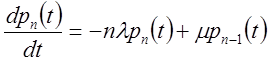
Початкові умови ![]()
![]() ,
, ![]() ,
,
У початковий момент усі канали вільні.
При ![]() режим роботи СМО, для
якого імовірності станів визначаються формулами Ерланга:
режим роботи СМО, для
якого імовірності станів визначаються формулами Ерланга:
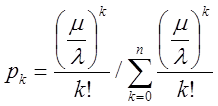 .
.
(![]() — можна обчислити за допомогою
таблиць пуасонівського розподілу)
— можна обчислити за допомогою
таблиць пуасонівського розподілу)
Імовірність, що заявка буде обслуговуватися (не одержить відмовлення) виражається формулою
![]()
Для СМО з обмеженням по числу місць у черзі щільності імовірності виражаються формулами
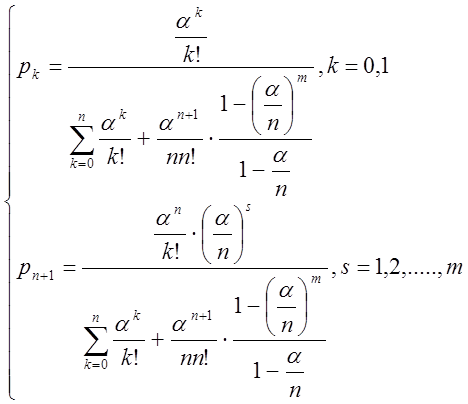
Де
![]() — число каналів обслуговування
— число каналів обслуговування
![]() — число місць у черзі;
— число місць у черзі; 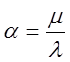
![]() — щільність потоку
заявок
— щільність потоку
заявок
![]() — щільність потоку
обслуговування однієї заявки
— щільність потоку
обслуговування однієї заявки
Для системи з чеканням ![]() обмежений
режим існує тільки при
обмежений
режим існує тільки при 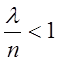 . На кожну заявку, що
знаходиться в черзі діє “потік відходів” із щільністю
. На кожну заявку, що
знаходиться в черзі діє “потік відходів” із щільністю ![]() ,
прирівняної до середнього часу в черзі.
,
прирівняної до середнього часу в черзі.
Приклад. Розглядається робота ЕОМ. Середня година безвідмовної
роботи ЕОМ дорівнює ![]() ; (потік відмовлень з
параметром
; (потік відмовлень з
параметром ![]() ). Якщо в ЕОМ відбувається збій, то вона
зупиняється і ремонтується. Середній час ремонту
). Якщо в ЕОМ відбувається збій, то вона
зупиняється і ремонтується. Середній час ремонту ![]() , потік
відновлення **** з параметром
, потік
відновлення **** з параметром ![]() ; Визначити імовірність
того, що ЕОМ буде працювати в момент
; Визначити імовірність
того, що ЕОМ буде працювати в момент ![]() , якщо в
момент
, якщо в
момент ![]() вона працювала.
вона працювала.
Рішення.
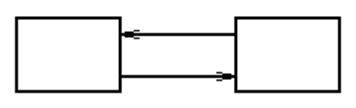
Розглянемо два стани ЕОМ:
![]() — у робочому режимі
— у робочому режимі
![]() — ремонтується.
— ремонтується.
Імовірність цих станів у момент ![]() позначимо
позначимо ![]() і
і ![]()
Створимо граф імовірностей
 |
|
|||||||
|
|
||||||
Система диференціальних рівнянь:
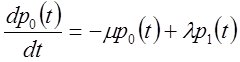 ;
;
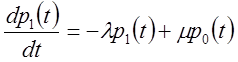 .
.
Рішення системи рівнянь при початкових умовах
![]()
![]() буде
буде
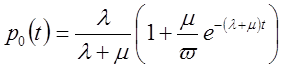 ;
;
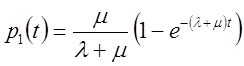 .
.
Для ![]() буде стаціонарний режим
роботи системи з імовірностями.
буде стаціонарний режим
роботи системи з імовірностями.
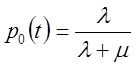
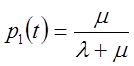 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.