Расчет металлорежущих станков. Выпуск третий: Конспект лекций, страница 7

Далее определяем удельное давление  в за­висимости от внешней нагрузки и основных размеров шпиндельной бабки. Для этого сделаем подстановку значений в уравнение (13). Имеем:

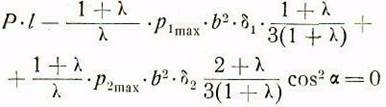
или после сокращения:

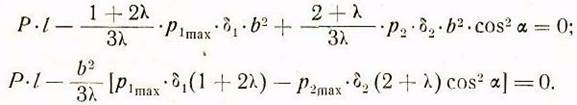
На основании (12) приравниваем

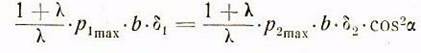
или после сокращения

Отсюда делаем подстановку в предыдущее уравнение, в результате имеем:

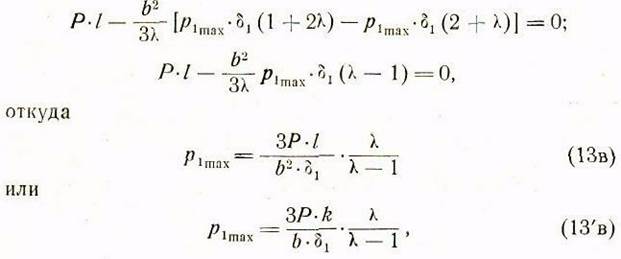
где имеют прежние значения.

Из (136) следует, что

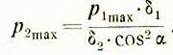
Подстановка в правую часть этого равенства дает:

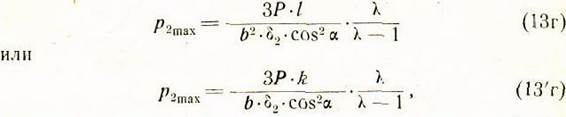
где k имеет прежнее значение. Формулы (13'в) и (13'г) с учетом (13а) позволяют рассчитать удельные давления на передних и задних гранях направляющих по заданным  и внешней нагрузке Р. Формула (13'г) позволяет также определить длину направляющих b по заданным

б) Расчет на устойчивость шпиндельной бабки

Для расчета на устойчивость шпиндельной бабки восполь­зуемся уравнением (11). Из этого уравнения следует, что:

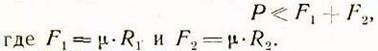
Коэффициент устойчивости определится как

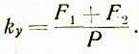
Значения        определены выше;

§ 13. Шпиндельные гильзы сверлильных станков

1) Определение удельных давлений на поверхности гильзы

Часто сверлильные станки строятся таким образом, что шпиндельная бабка укрепляется на станине неподвижно, а движение подачи осуществляет цилиндрическая гильза с рей­кой на внешней стороне шпиндель, Причем гильза совершает только поступательное движение, а шпиндель, помещенный внутри гильзы — поступательное и вращательное. Такое уст­ройство механизм подачи имеет не только в вертикальносвер-лильных, но и радиальносверлильных станках.

Рассматривая поступательное движение гильзы, опреде­ляем максимальное удельное давление на цилиндрической по-

верхности гильзы. Для этого обращаемся к расчетной схеме, приведенной на рис. 8. Из рассмотрения этой схемы следует соотношение:

где — некоторая величина износа, принимаемая постоянной в направлении действующей силы . С дру­гой стороны, величина износа может быть выражена так:

Приравнивая правые части последнего и предыдущего ра­венств, можно написать:

Отсюда следует, что

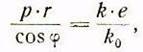
откуда удельное давление

Сумма проекций всех удельных давлений, действующих на цилиндрическую поверхность гильзы, на диаметральную плос­кость, должна уравновешиваться с радиальным усилием

На этом основании составляется уравнение (рисунок 5в);

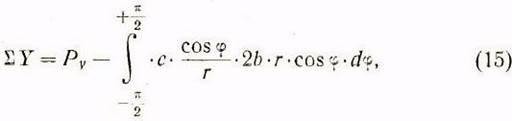
где —элементарная поверхность. Уравнение (15) записываем в иной форме и решаем интеграл:

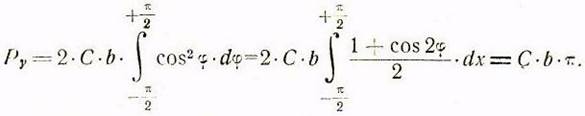
Таким образом, постоянная С равна:

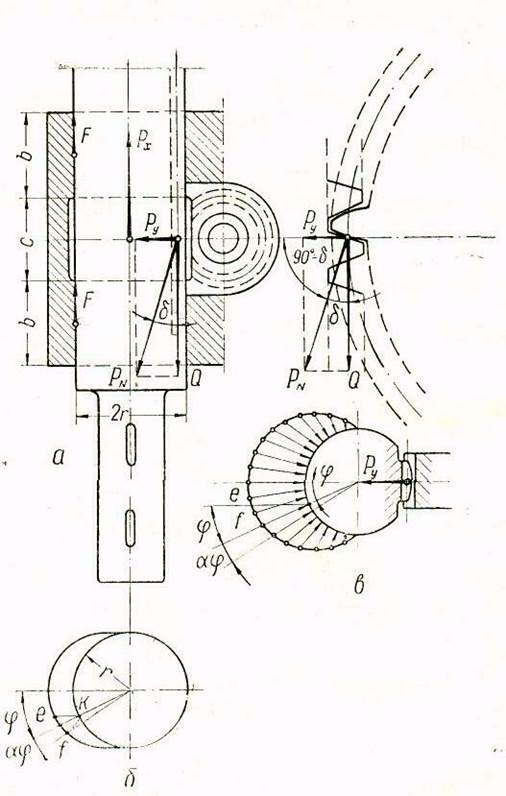
Рис. 8. Расчетная схема к определению основных разме­ров гильзы и тяговой силы, необходимой для подачи шпинделя при неподвижно укрепленной шпиндельной бабке на станине сверлильного станка

Учитывая формулы (14) и (15а), определяем удельное давление в таком виде:

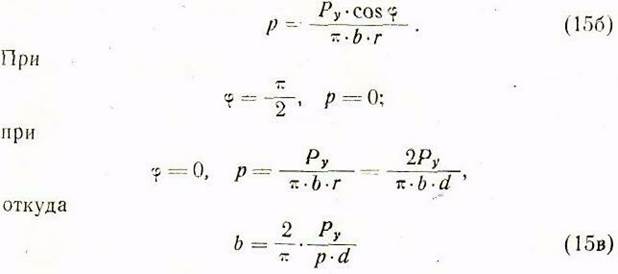
2) Определение тяговой силы, необходимой для перемещения гильзы со шпинделем в осевом направлении при сверлении

При подаче гильзы со шпинделем во время сверления, воз­никает осевая сила резания при сверлении  и силы трения на поверхности цилиндрических направляющих, на поверхно­сти зуба вследствие существования давления на него со сто­роны реечной шестерни, сила трения в шлицах шпинделя станка.

Учитывая эти условия, составляем уравнение равновесия:

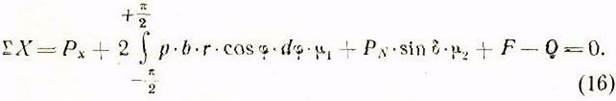
Здесь F—сила трения на шлицевых поверхностях шпин­деля, которую можно определить как

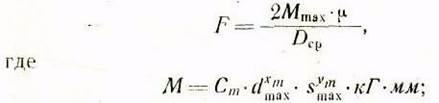
— максимальный диаметр сверла в мм;

— максимальная подача в мм об,

Подставляя значение p из уравнения (156) в уравнение (16). производим необходимое сокращение и преобразование;

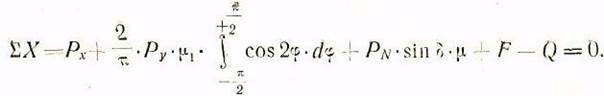
Решение интеграла приводит к уравнению:

На основании рис. 8 выражаем через Q:

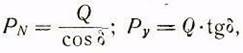
где— нормальное усилие, действующее на зуб шестерни, сцепляющейся с рейкой.

Подставляя значенияв уравнение (16а) и решая его относительно усилия а, движущего гильзу со шпинделем, получаем расчетную формулу:

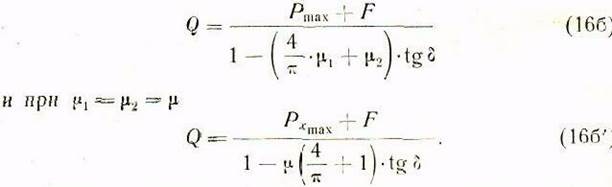
Исходя из усилия/определяемого формулой (16'б), следу­ет производить расчет на прочность зубьев шестерни и рейки.

3) Расчет модуля зубьев реечной передачи

Известно, что усилие, допускаемое прочностью одного зуба, определяется по формуле:

где

у — коэффициент формы зуба, учитывающий раз­меры опасного сечения;

 —рабочая ширина шестерни по начальному ци­линдру в мм;

— шаг зубьев в мм;

m—модуль нормальный;