Расчет металлорежущих станков. Выпуск третий: Конспект лекций, страница 17

— числа заходов червяков и числа зубьев червячных колес;

— числа зубьев шестерен постоянных пе­редач.

При аналитическом расчете коробки подач со сменными колесами но рис. 23 воспользуемся уравнениями, выражающими подачи. Для этого производим деление указанных уравнений почленно. Так, разделив первое уравнение па шестое, получим:

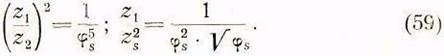
Деление второго уравнения на пятое дает:

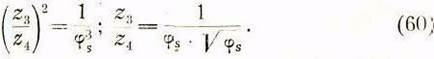
После деления третьего уравнения на четвертое имеем:

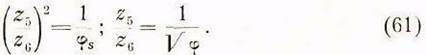
Недостающие уравнения составляем, учитывая неизмен­ность расстояния между осями сменных колес:

В результате имеем пять уравнений с шестью неизвестны­ми числами зубьев. Одним лишним неизвестным задаемся на основе конструктивных соображений. Таким неизвестным чис­лом зубьев является  Путем совместного решения уравне­ний (59)— (63) определяем значения чисел зубьев шестерен

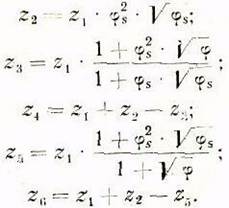
После того, как определены числа зубьев сменных шесте­рен, рассчитываются элементы постоянных передач, пользу­ясь одним из уравнений, которые выражают подачи. Прини­маем уравнение для  Переписываем это уравнение в таком виде:

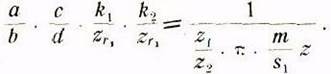
Введем обозначение знаменателя правой части последнего равенства:

после чего можно записать его в таком виде:

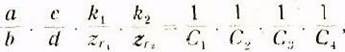
откуда:

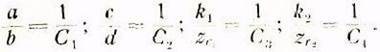
Отсюда получаем значения

В данном расчете, как и в предыдущих, принимаем , а значение    определяем как отношение:

В результате имеем пять уравнений с шестью неизвестны­ми числами зубьев. Одним лишним неизвестным задаемся на основе конструктивных соображений. Таким неизвестным чис­лом зубьев является  Путем совместного решения уравне­ний (59)— (63) определяем значения чисел зубьев шестерен

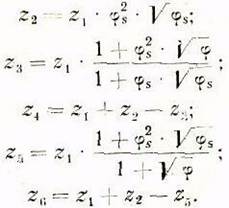
После того, как определены числа зубьев сменных шесте­рен, рассчитываются элементы постоянных передач, пользу­ясь одним из уравнений, которые выражают подачи. Прини­маем уравнение для  Переписываем это уравнение в таком виде:

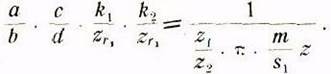
Введем обозначение знаменателя правой части последнего равенства:

после чего можно записать его в таком виде:

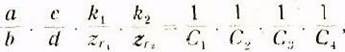
откуда:

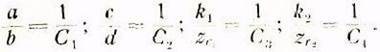
Отсюда получаем значения

В данном расчете, как и в предыдущих, принимаем , а значение    определяем как отношение:

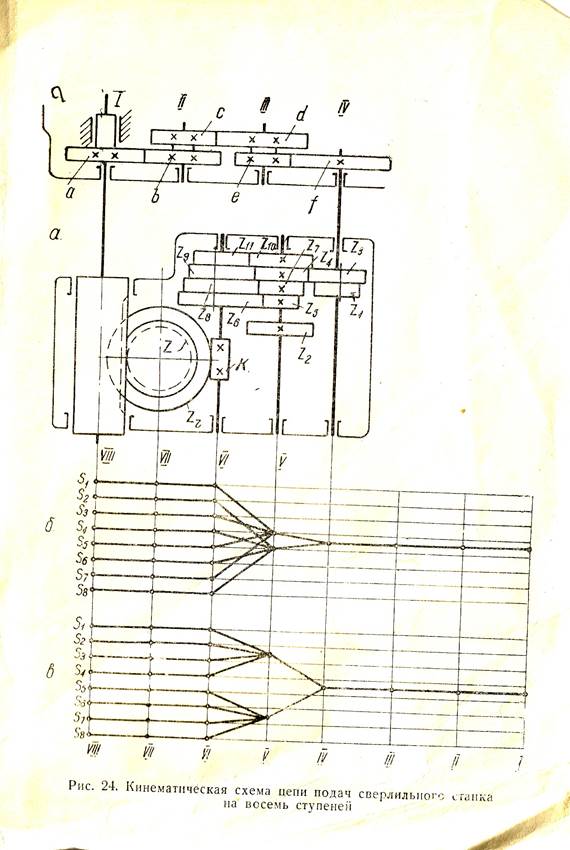
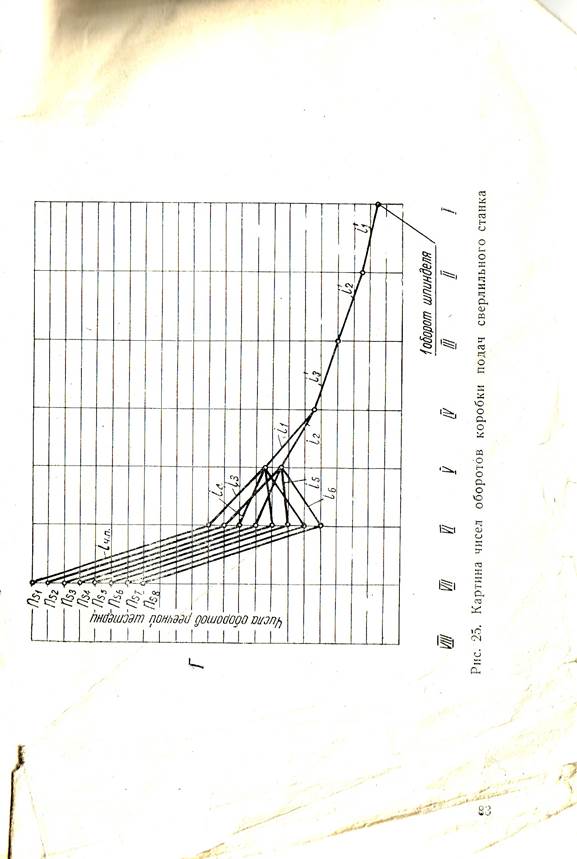
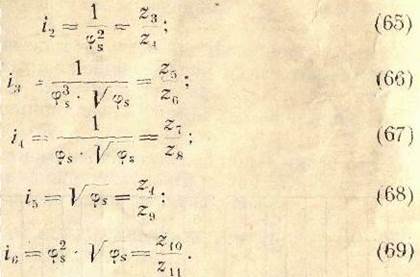
Недостающие уравнения составляем, учитывая условия па­раллельности осей шестерен:

Таким образом, получили десять уравнений с одиннад­цатью неизвестными числами. Зададим число зубьев одной из шестерен, руководствуясь конструктивными соображениями. Принимаем за известное число зубьев ведущей шестерни  двухшестеренного блока. Решая совместно уравнения (64)-:-(73), рассчитываем числа зубьев шестерен

Из уравнения (64) находим:

Подстановка значений в (70) дает:

откуда

и соответственно

Из уравнения (68) число зубьев

Используя уравнения (66) и (71), определяем значения чисел зубьев . Из (66) имеем:

Производим подстановку  в правую часть равенства (71) и решаем относительно

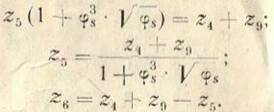
Значения  определяем из уравнений (67) и (72) тем же методом. Имеем после подстановки:

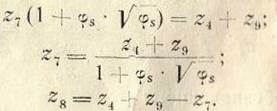
Значения чисел зубьев шестерен  рассчитываем,

пользуясь уравнениями (69) и (73);

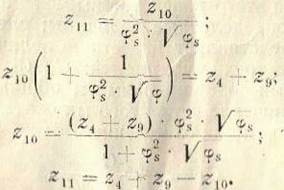
Постоянные передачи кинематической цепи подач рассчитываются, пользуясь одним из уравнений, которые выражают подачи:

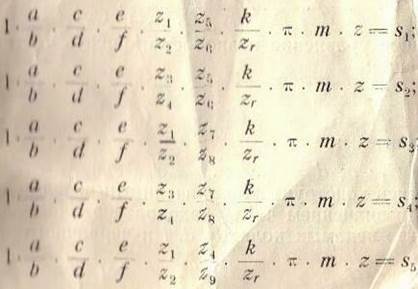
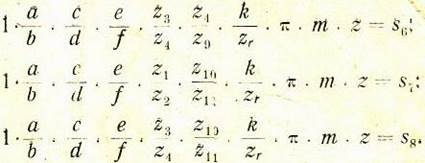
Для расчета постоянных передач переписываем уравнение, выражающее  в таком виде:

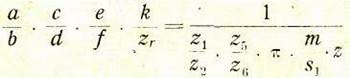
и затем вводим обозначение:

где левая сторона этого равенства выражена через известные. предварительно определенные величины; следовательно, пра­вая часть его представляет известную величину. Здесь зада­емся значениями трех множителей: , сообразуясь с конструктивными соображениями и общим значением про­изведения С, а значение четвертого множителя для червячной передачи определяем как отношение.           

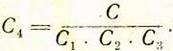
Имея в виду принятые обозначения, предыдущее уравне­ние можно записать в такой форме:

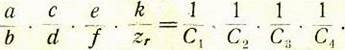
Это общее уравнение позволяет написать частные расчет­ные уравнения:                                     

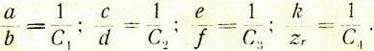
Отсюда имеем:

Задавшись конструктивно значениями чисел зубьев  шестерен а, с, e и значением числа заходов червяка, рассчитываем числа зубьев ведомых колес b, d, f и червячного колеса

---------------