Расчет металлорежущих станков. Выпуск третий: Конспект лекций, страница 5

Так как коэффициент устойчивости определен из условия равновесия шпиндельной бабки, то очевидно его числовая ве­личина должна быть равна единице. Покажем это на конкрет­ном примере. Для этого произведем числовой расчет. В су­ществующих станках отношение kизменяется в пределах  Принимая значение  и значение коэффициента трения  определяем отношение удель­ных давлений  по формуле (7'б).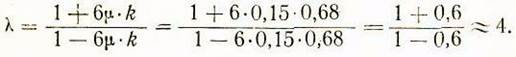

Таким образом, для равновесия шпиндельной бабки дол­жно быть

Соответственно коэффициент устойчивости шпиндельной бабки будет равен:

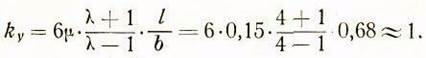
Затем, задавшись шириной соприкосновения задних гра­ней  и длиной направляющих  а также максимальным осевым усилием Р шпиндельной бабки, рассчитаем макси­мальное удельное давление на этих гранях.

Принимаем:

Подставляя эти значения, а также в формулу(7'д), найдем, что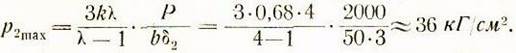

Определенное таким образом контактное напряжение (удельное давление на задних гранях направляющих) лежит

в пределах допускаемых напряжений. Это напряжение не­сколько превышает допускаемое при малых скоростях, поряд­ка скоростей подачи в токарных фрезерных и аналогичных станках.

Заметим, что значение  определено для неподвижно укрепленной шпиндельной бабки, находящейся в равновесии, когда коэффициент устойчивости

Для большей надежности работы станка коэффициент устойчиво­сти при максимальной осевой нагрузке должен быть  Мы полагаем, что это должно быть достигнуто путем приня­тия повышенного значения коэффициента затяжки винтов при их расчете и соответственно при установке шпиндельной баб­ки на станине путем затяжки ее винтами. Соответственно это вызывает повышение контактных напряжений предваритель­ного натяга соприкасающихся поверхностей, а следовательно, и повышение максимальных контактных напряжений.

Так при

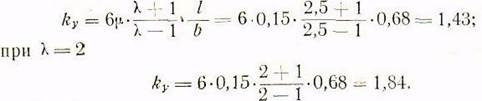
Соответственно при

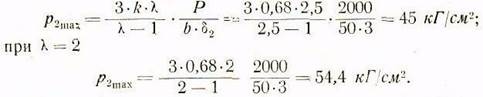
Таким образом, максимальное контактное напряжение на задних гранях направляющих может увеличиться до 45— 55 кГ/см², что для контактирующихся поверхностей неподвиж­ного кронштейна, каковым является шпиндельная бабка, мож­но считать допустимым.         

2. СТАНИНА, НА КОТОРУЮ УСТАНАВЛИВАЕТСЯ ШПИНДЕЛЬНАЯ БАБКА. ИМЕЕТ ПЛОСКИЕ КОСОУГОЛЬНЫЕ НАПРАВЛЯЮЩИЕ

1) Шпиндельная бабка совершает поступательное движение подачи вдоль направляющих при сверлении

На рис. 6 изображена шпиндельная бабка сверлильного станка с косоугольными направляющими, совершающая по­ступательное движение при его работе, в двух проекциях.

Шпиндель вращается в гильзе и поступательно движется вместе с гильзой и шпиндельной бабкой вдоль направляющих.

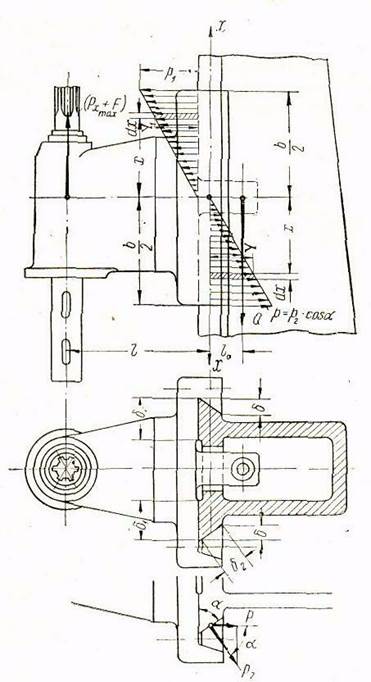
Рис. 6. Расчетная схема к определению основных размеров плоских косоугольных направляющих и тяговой силы шпиндельной бабки.

На том же рисунке представлена расчетная схема, позво­ляющая вывести зависимости для определения основных раз­меров направляющих.

а) Вывод зависимостей для определения основных размеров направляющих и тяговой силы

На рис, 6 показано, что при движении шпиндельной бабки под действием тяговой силы Q преодолевается осевая сила  ,  представляющая собой сопротивление внедрению сверла в металл, кроме того, преодолевается сила трения на гранях шлицов шпинделя и сила трения на плоскостях на­правляющих станины.

Принимаем характер распределения удельных давлении (контактных напряжений) на направляющих плоскостях ана­логично тому, как это сделано в случае рассмотрения задачи с плоскими прямоугольными направляющими, а именно, при­нимаем на передних плоскостях направляющих удельное дав­ление , в середине длины b, равным нулю, и изменяющимся по прямолинейному закону до  в крайней верхней точке.

Аналогично принято распределение — проекции удель­ного давления от середины вниз на скошенной направляющей плоскости до  (плоскости симметрии станины), Уравнение проекций сил на ось х:

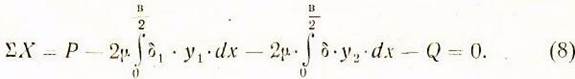
Уравнение проекций сил на ось у:

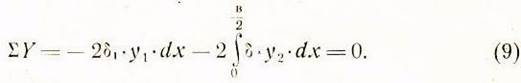
Уравнение моментов сил относительно точки О:

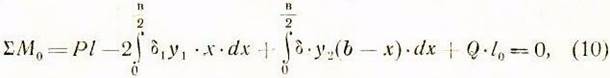
где согласно рис. 8 определяются значения

Сделав подстановку этих значений в уравнения (8) / (10), будем иметь:

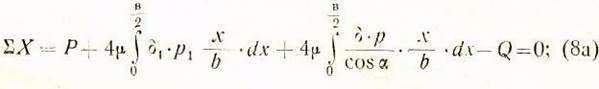
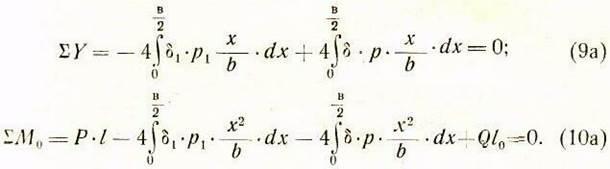
Выполнив интегрирование выражений, входящих в урав­нения (8а) — (10а) и соответствующие упрощения, получим:

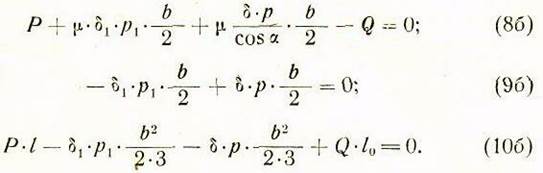
Решаем эти уравнения совместно и выводим формулы для определения удельных давлений и тяговой силы.