Расчет металлорежущих станков. Выпуск третий: Конспект лекций, страница 3

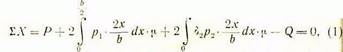
где

.

Уравнение проекций сил на горизонтальную ось:

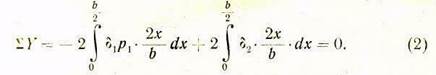
Уравнение моментов сил, действующих на шпиндельную с бабку, относительно точки :

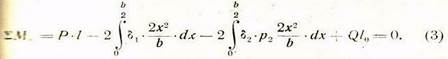
 После определения интегралов, входящих в уравнения (1), (2) и (3),получаем уравнения:

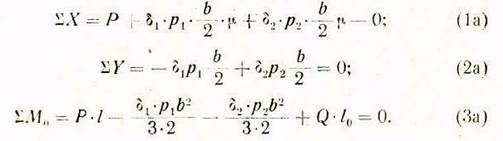
Из уравнения (2а), после сокращения на  можем написать, что

Отсюда, сделав подстановку  в уравнения (1а) и (За), получим

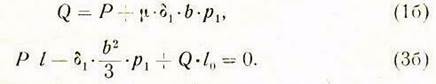
Таким образом, имеем два уравнения с двумя неизвестными  и  . Решаем эти уравнения совместно. Подставляем значение  из уравнения (16) в уравнение (36), в результате имеем:

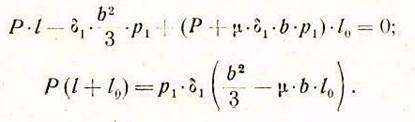
Отсюда контактное напряжение  на передних гранях на­правляющих определяется в зависимости от нагрузки , основных размеров направляющих шпиндельной бабки в следу­ющем виде:

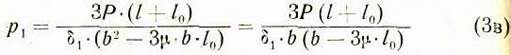
и соответствующее контактное напряжение  на задних гра­нях направляющих, учитывая равенство (2б):

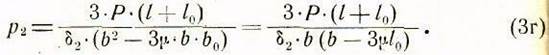
Подставляя значение  в уравнение (1), получим расчетную формулу для определения тяговой силы  , под дей­ствием которой шпиндельная бабка совершает движение по­дачи, в зависимости от внешней нагрузки  и основных раз­меров направляющих шпиндельной бабки:

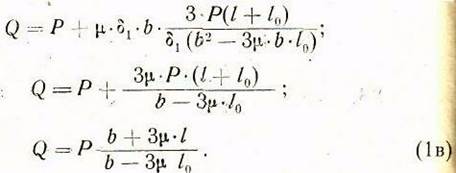
Поделив числитель и знаменатель правой части послед­него равенства на b получим в окончательном виде расчетную формулу для определения тяговой силы:

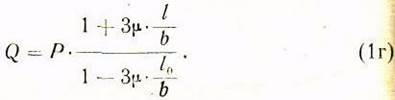
б) Расчет регулирующих винтов направляющих планок

Определение усилий, действующих на направляющие планки

Переходим к определению усилий, действующих на направляющие планки и регулирующие винты. При этом поль­зуемся расчетной схемой, которая изображена на рис. 2. В верхней части слева (на этой расчетной схеме) показана диаграмма контактных напряжений в таком виде, как на пре­дыдущем рисунке, а в правой части схемы показаны усилия

 , действующие на планку, а следовательно, на шпиндельную бабку, так как планка привинчена к последней, то представляет с ней одно жесткое тело.

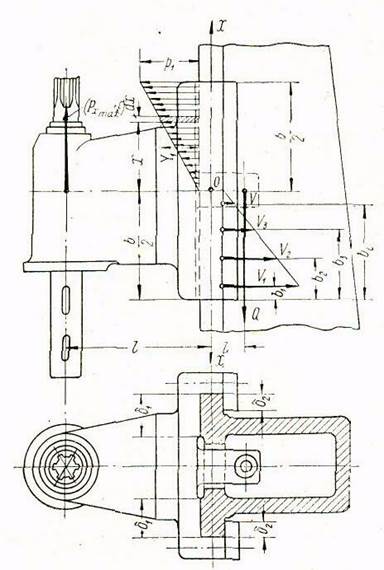
Рис. 2. Расчетная схема к определению усилий, действующих на вспомогательные грани (план­ки) прямоугольных направляющих шпиндельной бабки (кронштейна) сверлильного станка.

Составляем уравнения равновесия сил, действующих на шпиндельную бабку, по рис. 2.

Уравнение моментов сия относительно точки О определяется в таком виде:

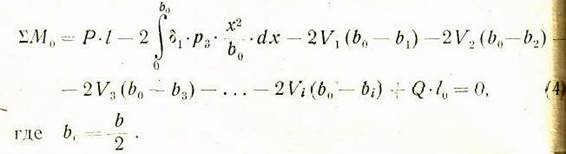
Решая интеграл в предыдущем уравнении, получим:

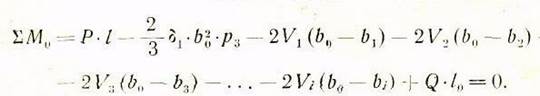
Используя свойство подобных треугольников, можем напи-сать, что

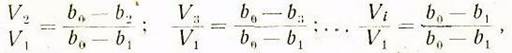
откуда

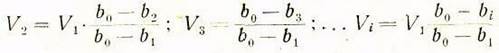
После подстановки значений  в уравнение моментов (6а) будем иметь:

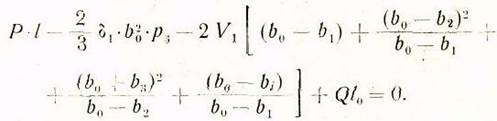
Отсюда находим усилие, действующее на направляющую планку:                                       

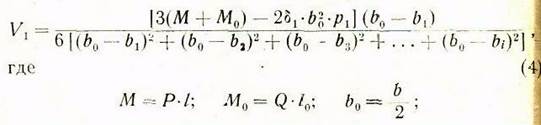
значение  определяется по формуле (1в) или (1а).

Сделав подстановку значения  в правую часть равенства

изменяются по закону треугольника, начиная от нуля у од­ного края кронштейна и достигая максимума у другого. В том же виде допущение переносилось и на расчет шпиндельной бабки, которая представляет собой кронштейн. Однако чис­ловой расчет на устойчивость и опытная проверка работы шпиндельной бабки сверлильных станков под нагрузкой по­казывает, что такое допущение не удовлетворяет требованиям устойчивой ее работы.

По данному вопросу пока еще нет надежных сведений в научно-технической литературе, не проверены надлежащим образом существующие теоретические исследования, отсут­ствуют специальные эксперименты. Тем не менее нам ясно, что до приложения максимальной осевой нагрузки натяг за­жимных планок должен вызывать удельные давления (и со­ответственно контактные напряжения) по величине более вы­сокие, чем  на передних гранях и  на задних гранях направляющих. Последнее указывает на то, что зако­ном изменения удельных давлений на гранях направляющих должен быть не треугольник, а трапеция.

а) Вывод зависимостей для определения основных размеров     направляющих шпиндельной бабки сверлильного станка

Па рис. 4 представлена расчетная схема, пользуясь кото­рой, производим вывод формул для определения основных размеров направляющих и расчета шпиндельной бабки на устойчивость. На рисунке представлена шпиндельная бабка в двух проекциях. Здесь показаны силы, действующие на нее.

Внешними силами являются осевая сила  и сила трения