Из рис. 6 можем написать, что
![]()
и соответственно
![]()
а также на основании (96) найдем, что
![]()
Подставляя эти значения в (86), будем иметь:
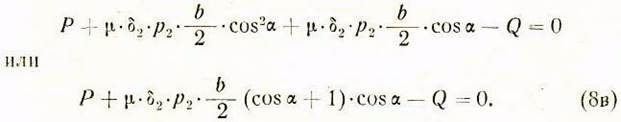
Аналогичная подстановка в уравнение (106) дает:
![]()
откуда удельное давление
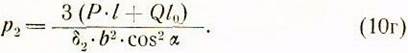
При ![]() формула принимает вид, соответствующий
прямоугольному сечению направляющих.
формула принимает вид, соответствующий
прямоугольному сечению направляющих.
Делаем подстановку ![]() в (8в) и соответствующее сокращение, после чего
приходим к уравнению:
в (8в) и соответствующее сокращение, после чего
приходим к уравнению:
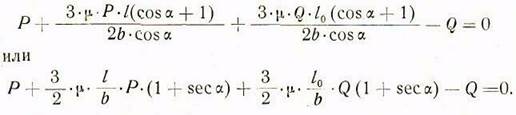
Отсюда расчетная формула для определения тяговой силы необходимой для перемещения шпиндельной бабки, выражается в таком виде:
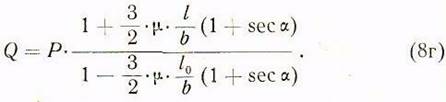
Подставляя значение тяговой силы Q из (8г) в правую часть равенства (10г), в результате получаем формулу для определения удельного давления:
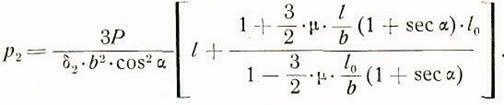
Преобразование и упрощение этой формулы приводит к следующему ее виду:
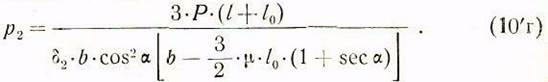 В случае прямоугольных
направляющих угол
В случае прямоугольных
направляющих угол ![]()
![]() и соответствующая расчетная
формула удельного давления будет:
и соответствующая расчетная
формула удельного давления будет:
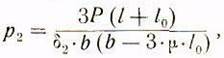
которая имеет идентичный вид с (Зг).
При ![]() формула (8г) для Q
принимает вид (1г), соответствующий случаю, когда направляющие имеют прямоугольное
сечение.
формула (8г) для Q
принимает вид (1г), соответствующий случаю, когда направляющие имеют прямоугольное
сечение.
Косоугольные
направляющие в поперечном сечении имеют угол ![]() , что соответствует
, что соответствует ![]()
![]()
При этом значении угла
![]() формула (8г) принимает
вид:
формула (8г) принимает
вид:
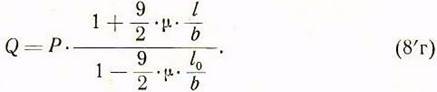
Определив
тяговую силу по предварительно найденному значению Р и
намеченным параметрам ![]() а
также задавшись шириной скошенной грани направляющих
а
также задавшись шириной скошенной грани направляющих ![]() определяем удельное давление
определяем удельное давление ![]() пользуясь формулой (8 г). Найденное таким образом удельное давление сопоставляется с допускаемым. Так обычно поступает
опытный конструктор. Можно поступить и наоборот: задаться
пользуясь формулой (8 г). Найденное таким образом удельное давление сопоставляется с допускаемым. Так обычно поступает
опытный конструктор. Можно поступить и наоборот: задаться ![]() и определив предварительно Р и
Q, рассчитать ширину скошенной
грани направляющих но формуле:
и определив предварительно Р и
Q, рассчитать ширину скошенной
грани направляющих но формуле: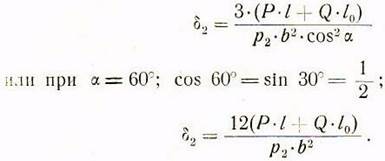
Для угла ![]() формула для Q принимает вид (1г),
которая выведена для прямоугольных направляющих.
формула для Q принимает вид (1г),
которая выведена для прямоугольных направляющих.
Приняв значение ![]() формула (8г) будет иметь вид:
формула (8г) будет иметь вид:
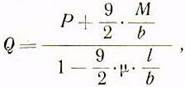
Формула, выражающая удельное давление, в этом случае выразится так:
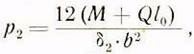
где Q
— тяговая сила; ![]()
2) Шпиндельная бабка укреплена на станине неподвижно при работе сверлильного станка
Вертикальносверлильные станки небольших и средних размеров имеют косоугольные направляющие станины, для установки шпиндельной бабки. Причем шпиндельная бабка устанавливается на станине неподвижно при работе станка.
Ниже приводится рассмотрение устойчивого равновесия шпиндельной бабки с применением основных положений механики и резания металлов при сверлении на станке и выводятся расчетные формулы для определения основных параметров кронштейна.
а) Вывод зависимостей для определения основных размеров направляющих шпиндельной бабки сверлильного станка
На рис. 7 изображена расчетная схема, позволяющая определить основные размеры направляющих и расчет шпиндельной бабки на устойчивость.
В принципе на шпиндельную
бабку по рис. 7 действуют те же силы, что и по рис. 4. Разница только в том,
что в вертикальной плоскости мы имеем проекцию ![]() а в случае прямоугольных направляющих реакция
а в случае прямоугольных направляющих реакция ![]() проектируется в натуральную
величину в той же плоскости.
проектируется в натуральную
величину в той же плоскости.
Учитывая сказанное, составляем уравнение равновесия сил, действующих на шпиндельную бабку:
![]()
где Р—имеет прежнее значение;
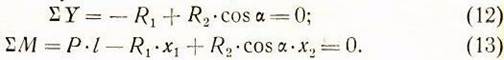
Из уравнения
(12) следует, что![]() На этом
основании уравнение (11) можем записать так:
На этом
основании уравнение (11) можем записать так:
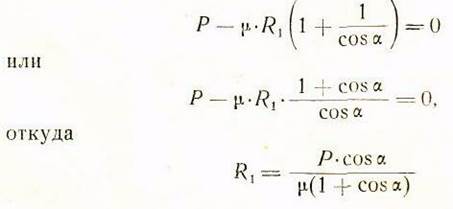
и соответственно
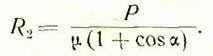
|
Выражаем
значения |
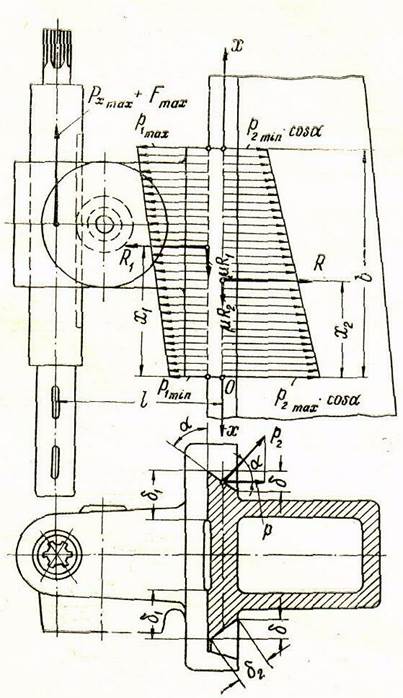
Рис. 7. Расчетная схема к определению основных размеров плоских косоугольных направляющих. Шпиндельная бабка укреплена неподвижно на станине сверлильного станка.
Из рассмотрения эпюры удельных давлении на гранях направляющих следует, что
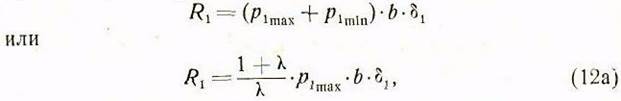
где ![]() —имеет прежнее значение [см.
(6а), (13а)]
—имеет прежнее значение [см.
(6а), (13а)]
Аналогично определяется значение реакции ![]()
![]()
где
![]() —приведенная ширина
задней грани. Координаты центров давлений на задних гранях направляющих
определяются так же, как и в случае прямоугольных направляющих, а именно
(см.стр.17).
—приведенная ширина
задней грани. Координаты центров давлений на задних гранях направляющих
определяются так же, как и в случае прямоугольных направляющих, а именно
(см.стр.17).
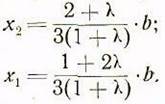
Значение ![]() определяем в зависимости от l и b. Подставляем значения
определяем в зависимости от l и b. Подставляем значения ![]() а также
а также ![]() в уравнение (13), в результате
получаем:
в уравнение (13), в результате
получаем:
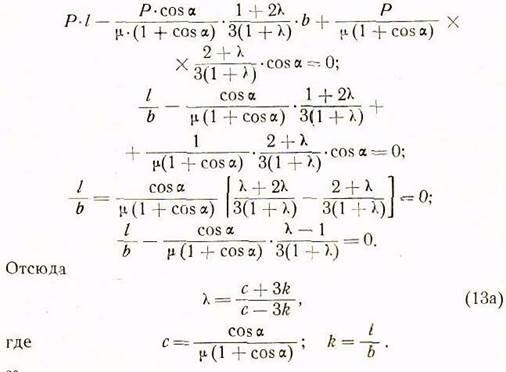
При ![]() ,тогда значение
,тогда значение ![]() принимает вид (76), что соответствует
прямоугольным направляющим.
принимает вид (76), что соответствует
прямоугольным направляющим.
Значения l и b показаны на рис. 7.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.