Так как С постоянна для данного слоя, f(C) и f'(C) имеют постоянное значение и поэтому U должно быть также постоянной. Постоянство может быть использовано для определения твердого на верхней границе осаждающейся пульпы. Пусть Со и Но - соответственно исходные концентрации и высота столба пульпы в опыте по осаждению. Тогда общий вес твердого в этом столбе пульпы будет СоНоS. Когда любой слой с определенной концентрацией твердого достигнет поверхности раздела вода-пульпа, все количество твердого в столбе, вероятно, уже пройдет через него, так как слой распространяется вверх от нижней части столба. Если концентрация этого слоя С2 и если этот слой достигнет поверхности раздела за время t2, то количество твердого, проходящего через этот слой C2St2(V2+U2), должно быть равно общему весу твердого в столбе пульпы, т.е.
CoHoS = C2St2(V2+U2)
Если Н2 представляет собой высоту сгущающейся пульпы в момент t2
и если, как было показано, скорость распространения вверх любого данного слоя - величина постоянная, то
U2
= 
Подставляя значение U2 в уравнение, получим после упрощения:
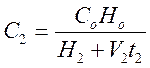
V2
равно 
в точке на кривой H=f(t),
отвечающей моменту, когда слой С2 доходит до поверхности пульпы.
Тогда тангенс угла наклона касательной и кривой в точке (Н2, t2)
— V2.
Из этого следует, что эта касательная пересекает ось Н в точке Н1 с координатою Н2 + V2t2. Заменяя в уравнении Н2 + V2t2 на H1, получим: С2H1 = СоНо. Отсюда следует, что Н1 -это высота, которую имела бы пульпа, если бы концентрация твердого в ней была равной концентрации в слое у поверхности раздела. Для любого произвольно выбранного значения С2 может быть вычисление соответствующее ее значение Н1. Затем может быть найдено значение как тангенса угла наклона касательной к кривой осаждения, проведенной через точку H1. Таким образом, по данным одного опыта можно построить зависимость V от С.
Простое геометрическое построение, показанное на рис. ...... , позволяет непосредственно получить значение удельной поверхности сгущения.
В момент t2 частицы в слое, существующем на поверхности пульпы, осаждаются с линейной скоростью (H1-H2):t2. Если частица этого слоя приобретают такую скорость, вода проходит мимо частиц, с объемной скоростью S(Н1-Н2):t2. B сгустителе частицы в любой зоне не могут осаждаться через все количество воды, так как часть этой воды выгружается вместе со сгущенным осадком. Количество воды, через которое они осаждаются, равно количеству воды, которое будет вытесняться при увеличении концентрации твердого до конечной. Соответствующее количество воды в условиях опыта будет S(H1-Hn), где Н1 высота пульпы, которая имела бы место, если бы концентрация твердого в пульпе была бы равна концентрации слоя, а Нn -высота пульпы при концентрации твердого в ней, равной концентрации в сгущенном шламе сгустителя. Тогда время, которое требуется для вытеснения S(H1-Hn) воды через слой с концентрацией С2, будет равно:
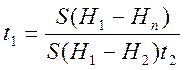
Из подобия треугольников следует, что
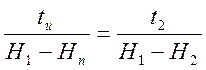
следовательно t' = tn .
Общее количество твердого в данном опыте равно СоHoS, а время, требующееся для прохождения этого количества твердого через слой с концентрацией С2 в сгустителе непрерывного действия, равно tn. Следовательно, количество твердого, которое может быть получено через концентрационный слой за единицу времени, равно СоHotu, Удельная площадь слоя есть площадь, требуемая для осаждения через концентрационный слой 1 т твердого в сутки.
Удельная площадь
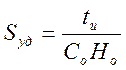
Для того, чтобы получить удельную площадь определенного сгустителя в квадратных метрах на тонну в сутки, надо в уравнении выразить t, Н и С соответственно в сутках, метрах и тоннах на кубический метр. Однако обычно удобнее строить кривую осаждения и выполнять графические построения в более удобных единицах, используя соответствующие преобразования.
Схемы промывки сгущенного продукта декантацией
Промывка сгущенного продукта (шлама, концентрата и т.д.) в системе сгустителей-промывателей методом противоточной декантации осуществляется по типичной схеме, представленной на рис........
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.