Приклади розв’язування деяких задач (Виразити складні події через елементарні події. Знайти всі додаткові умови відносно випадкових подій для запропонованої рівності)

ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ДЕЯКИХ ЗАДАЧ

1 Виразити складні події  через елементарні події  А – схема проводить струм,  - -тий елемент схеми проводить струм.

Зауваження

Вектор струму при проходженні схеми не може мати напрям справа – наліво.

1.1

Розв’язок

Виразимо подію А через події .

Спосіб 1. Виходимо з того, що подія А є сумою наслідків, які їй сприяють, причому кожний з цих наслідків складається з 5 еле­ментарних подій .

Маємо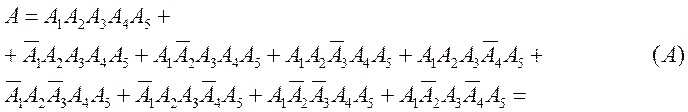

Перший доданок справа в (А) означає, що всі  5 елементів схеми проводять струм, чотири наступних – усі елементи схеми, крім одного, проводять струм; чотири останніх – усі елементи схеми , крім двох, проводять струм. Наступне спрощення виразу для по­дії А показано нижче, у фігурних дужках. Букву А у виразі, для спрощення і скорочення викладок, опущено.

Спосіб 2. Проглядаємо схему зліва – направо, враховуючи за­уваження, і включаємо в подію А всі послідовності подій , які приводять до “успіху”.

Маємо

Спосіб 3. Виходимо з того, що схема проводить струм, якщо елементи: 1 або 2 і, одночасно, 3 або 4 і, одночасно, 5 проводять струм. А це згідно з означенням суми і добутку двох подій озна­чає, що

Виразимо подію  через події . Це можна зробити способами 1 - 3. Наприклад, способом 2. Проглядаємо схему зліва — направо і включаємо в подію  усі послідовності події , які приводять до “успіху”:

А можна і ,використовуючи формули (закон двоїстості) де Мор­гана:

 Відповідь:

Зауваження

Відмітимо, що з розглянутих способів відшукання подій А і : два перших більш універсальні ніж третій, а з двох перших – другий менш громіздкий.

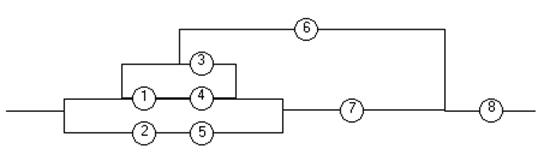
1.2

Розв’язок

Спосіб 2

При спрощенні події  в викладках у фігурних дужках опущено букву .

Відповідь:

Зауваження. Розглянуті вище (при розв’язанні задачі 1.1.) 3 способи відшукання події А і  звичайно не вичерпують усі можливості. Наприклад задачу 1.2. доцільно розв’язувати ком­бінуючи способи 2 і 3.

Маємо

Знайдемо також подію  для задачі 1.2., використовуючи фор­мули де Моргана:

2  Для запропонованої рівності, яка насправді не виконується, знайти всі додаткові умови відносно випадкових подій А,В,С  з яких би ця рівність випливала і які не зменшують область правильності рівності .

Зауваження. Задачу розв’язати із використанням таблиць істинності.

2.1.      

Розв’язок

	+	+	+	—	+	—	—	+	+	—
	+	—	+	+	+	—	—	+	+	—
+	—	+	+	—	—	+	+	+	—	+
	—	—	+	+	+	—	+	+	—	—
—	+	+	—	—	+	—	—	—	—	+
	+	—	—	+	+	—	—	—	—	—
+	—	+	—	—	—	+	+	+	—	+
	—	—	—	+	+	—	+	+	—	—
						*				*

Із порівняння відмічених зірочкою стовпців робимо висновок, що у відповідності із умовою задачі шукані додаткові умови повинні зберегти рядки, помічені знаком  “+”, оскільки в цих рядках події  і  відбуваються, і виключити рядок, помічений знаком “—”, оскільки в цьому рядку перша подія не відбувається, а друга – відбувається.

Помічений  знаком “—” рядок виключає умова  , оскільки їй відповідає ситуація: подія А відбулася (“+” у першому стовпці таблиці ), подія В відбулася (“+” у другому стовпці таблиці), а подія С ні (“—” у третьому стовпці таблиці), тобто ситуація відносно випадкових подій  А, В, С яка має місце вцьому рядку.

            Умова , оскільки подія  є суміщенням трьох випадкових подій, її множників, породжує також три наступних умови: , , . Тобто помічені знаком “—” рядок виключає будь-яка з умов

           

            Останній набір додаткових умов згідно із умовою задачі виписаний відносно випадкових подій А, В, С і події .

            Умова  (~) виключає один помічений знаком “—” рядок. Три інших умови, які містять лише по дві події з набору А, В, С виключають по два рядки таблиці істинності. Крім рядка поміченого знаком “—” умова  виключає перший рядок; умова  — сьомий рядок.

Оскільки за умовою задачі додаткові умови не повинні зменшувати область правильності рівності (це рядки помічені знаком “+”), то умову  з додаткових умов виключаємо.

Відповідь: ; ; .

2.2      

Розв’язок