Приклади розв’язування деяких задач (Виразити складні події через елементарні події. Знайти всі додаткові умови відносно випадкових подій для запропонованої рівності), страница 6

де  — число способів, якими можна вибрати  частинок з n можливих,  — число способів, якими можна вибрати  частинок з , залишившихся після першого випробу­вання, і т.д.

Отже

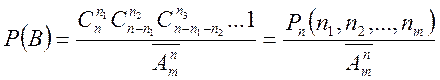
3 Шукаємо . Подію  можна подати в виді

(зміст подій  див. вище, розв’язок задачі 4.1).

Отже

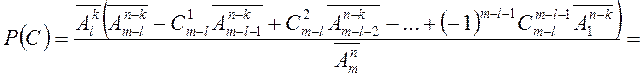
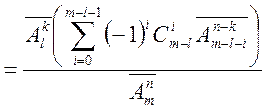
Спосіб 2

 Можна знайти  без обчислень окремо можливого числа наслідків і числа наслідків які спри­яють події.

Ймовірність для однієї частинки попасти в  ячейок з т можли­вих дорівнює відношенню , ймовірність для  розрізнимих *) частинок попасти в  ячейок з т можливих дорівнює 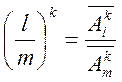. Тоді:

1 З урахуванням структури події , формула ,

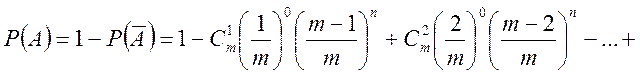
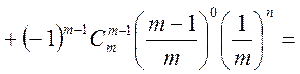
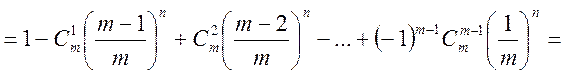
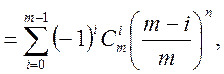
де 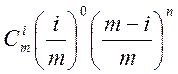 — ймовірність того, що  ячейок які можна вибрати з т можливих  способами пусті, тобто в них нуль частинок і всі  розрізнимих частинок розподіляються по всіх інших  ячейках.

2 З урахуванням структури події В

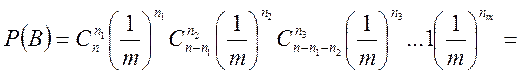
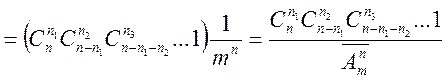
3 З урахуванням структури події С

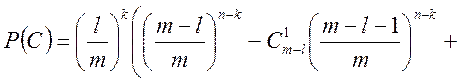
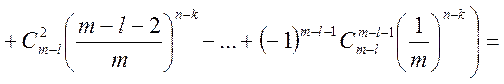
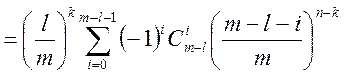
Відповідь: ;

;

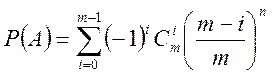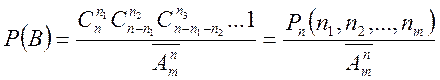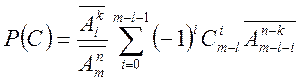
*) Зауваження

 Відмітимо, що для  нерозрізнимих час­тинок ця ймовірність буде такою:

 ,

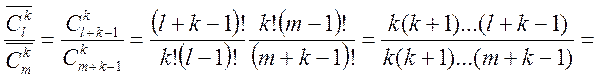
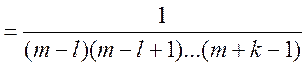тобто меншою в 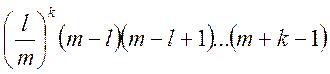 раз.

5 В урні 10 куль (і — білих і (10—і) — синіх). Із урни, навмання, способом  виймають кулі. Знайти ймовір­ність того, що серед вийнятих куль —  білих.

  —  раз виймають по одній кулі і повертають її назад;

  —  раз виймають по  куль і повертають їх назад;

 — виймають  куль не повертаючи їх назад;

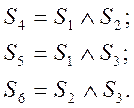
Додаткова інформація: а)  (або ), ; б)  (або ), .

5.1 а) 4,5,4,5; б) 4,6,3,2,6

Розв’язок

 Подамо коротко умову першої задачі а) ;  рази виймають по одній кулі і повертають її назад і виймають 4 кулі не повертаючи їх назад;  — потрібно знайти.

Нехай  — у випробуванні вийнято білу кулю, тоді подію , — подію задану умовою а) задачі, можна подати в виді

Перший доданок в А визначає наслідки в яких спочатку 4 рази виймають білі кулі, тоді, іншим спосо­бом, 1 раз білу і 3 рази не білу (чорну). Точка відокремлює різні способи виймання куль, множник  означає (або враховує), що цей доданок об’єднує 4 нас­лідки випробування. У одному з них біла куля з’явилася в 1, у другому – в 2, у третьому – в 3, у четвертому – в 4 випробуваннях. Зміст інших додатків в А аналогічний.

Враховуючи тепер, що доданки в А несумісні і, що в пер­шій серії випробування незалежні (випробування Бернуллі), а в другій залежні, маємо

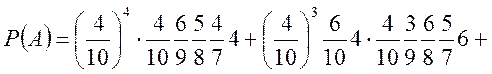
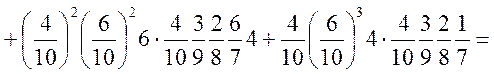
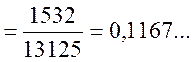
або

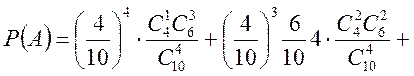
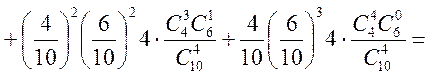
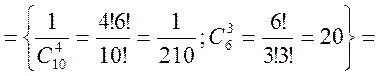
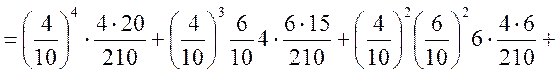
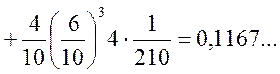
Подамо коротко умову другої задачі б)  — 3 рази виймають по 2 кулі і повертають їх назад і виймають 3 кулі не повертаючи їх назад;  — потрібно знайти.

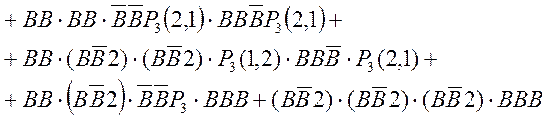
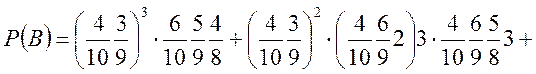
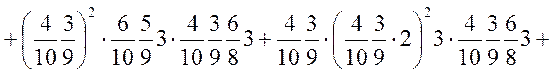
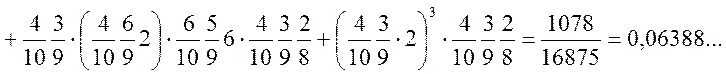
або

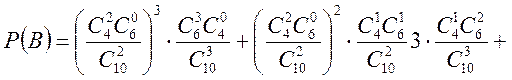
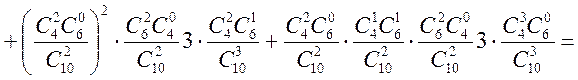
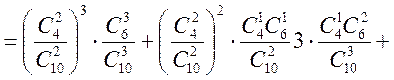
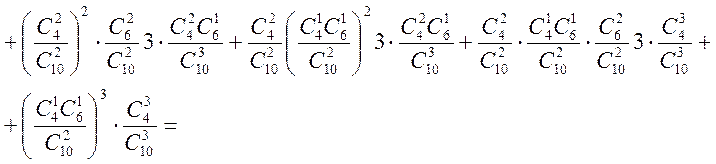
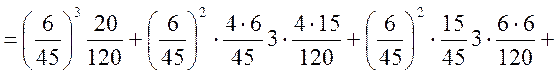
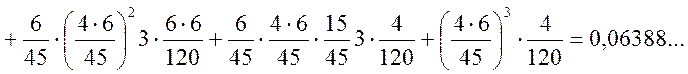
Зауваження

 Вище, при обчисленні  і  другим способом, обчислення ймовірності добутку залежних подій виконувалося за формулою

,

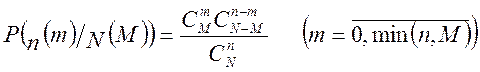де  — ймовірність того, що в  залежних ви­пробуваннях подія А настане рівно т раз при умові, що в  (за­лежних) випробуваннях вона настане рівно  раз.

Відповідь:

6 Точку кидають на площину  в область . Знайти ймовірність її попадання у підобласть  області.

Додаткова інформація: .

6.1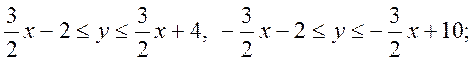

Розв’язок

 Перша подвійна нерівність задає полосу між па­ралельними прямими

1 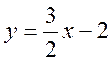            і   2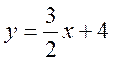       

друга – між паралельними прямими

3 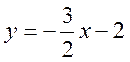             і   4    .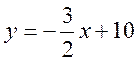

Отже вершини паралелограма, заданого двома зазначе­ними нерівностями, знайдемо розв’язуючи наступні системи рі­внянь.

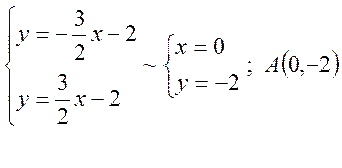
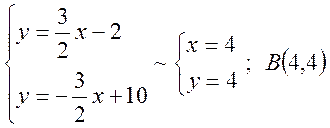
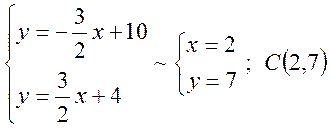
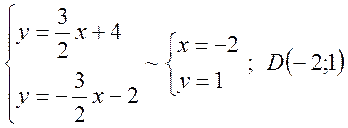
Наносимо на площині знайдені вершини паралелограма і будуємо сам паралелограм (область ).

Остання нерівність задає підобласть  області , обмежену всередині паралелограма кривою другого порядку. Знайдемо канонічне рівняння цієї кривої.

Т.ч. розглядувана крива – коло із центром у точці  і радіусом.

Знайдемо точку перетину кола із сторонами  і  паралелограма. Для чого розв’яжемо наступні системи рівнянь.

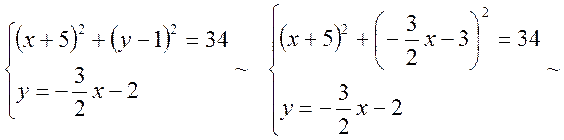
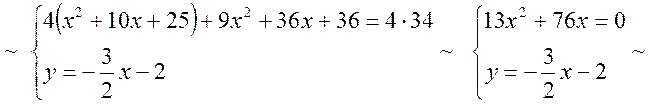
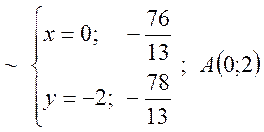
Друга точка лежить за межами області

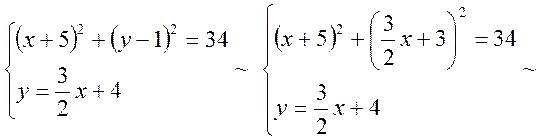
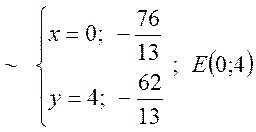
Друга точка лежить за межами області .

Наприклад точка  задовольняє нерівності

,

отже підобласть  лежить зліва від дуги  кола, і, оскільки,