Тоді
![]() .
.
Відмітимо, що тут, у ![]() , згідно
із змістом
, згідно
із змістом ![]() і
і ![]() враховано,
що в кожній з
враховано,
що в кожній з ![]() ячейок є по одній частинці а
інші
ячейок є по одній частинці а
інші ![]() частинок розподіляються по тих же
частинок розподіляються по тих же ![]() ячейках будь яким способом
ячейках будь яким способом
Отже
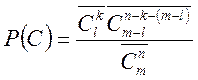
Спосіб 2
Знайдемо спочатку ![]() (
можливе число розподілів …). Розподіл n частинок по т ячейках
можна, наприклад, зобразити таким чином
(
можливе число розподілів …). Розподіл n частинок по т ячейках
можна, наприклад, зобразити таким чином
![]()
Тут нулі це частинки, а риски – проміжки між
ячейками, тобто, в ячейці 1 частинок розподілилося 3, в ячейці 2 — 0, в ячейці
3 — 2, в ячейці 4 — 1, в ячейці 5 — 0, …, в ячейці ![]() .
Усіх нулів n, рисок ‑
.
Усіх нулів n, рисок ‑ ![]() , тоді можливе число
розподілів n частинок по т ячейках буде дорівнювати числу
способів, якими можна вибрати n нулів серед
, тоді можливе число
розподілів n частинок по т ячейках буде дорівнювати числу
способів, якими можна вибрати n нулів серед ![]() нулів і
рисок, в середині між двома крайніми рисками, тобто
нулів і
рисок, в середині між двома крайніми рисками, тобто
![]()
1. Знайдемо тепер ![]() . Очевидно, що число таких розподілів буде
дорівнювати числу способів якими можна розмістити
. Очевидно, що число таких розподілів буде
дорівнювати числу способів якими можна розмістити ![]() внутрішню
риску в
внутрішню
риску в ![]() проміжках між нулями. Тобто
проміжках між нулями. Тобто
![]()
Отже
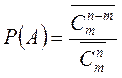
2. Події В сприяє лише один розподіл, отже
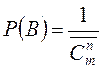
3. Подію С подаємо в виді
![]()
(зміст ![]() дивись вище). Тоді
дивись вище). Тоді
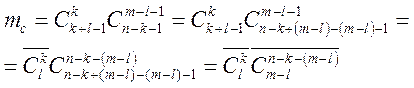 ,
,
де перший множник – це число способів, якими можна
вибрати ![]() нулів серед
нулів серед ![]() нулів і
рисок; другий множник це число способів якими можна розмістити
нулів і
рисок; другий множник це число способів якими можна розмістити ![]() внутрішніх рисок (тобто
внутрішніх рисок (тобто ![]() риску разом із
риску разом із ![]() нулями
між ними заміняємо однією рискою) в
нулями
між ними заміняємо однією рискою) в ![]() проміжках між нулями.
проміжках між нулями.
Отже

Відповідь:
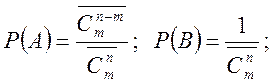

4 ![]() розрізнимих частинок розподіляються по
розрізнимих частинок розподіляються по ![]() ячейках.
ячейках. ![]() — будь-які (статистика Максвела —
Больцмана якій підкоряється ідеальний газ). Знайти ймовірності подій:
— будь-які (статистика Максвела —
Больцмана якій підкоряється ідеальний газ). Знайти ймовірності подій:
4.2
![]() — у кожній з ячейок є
хоча б одна частинка;
— у кожній з ячейок є
хоча б одна частинка;
![]() — у першу ячейку попала
— у першу ячейку попала
![]() частинка, у другу —
частинка, у другу — ![]() частинок, … , у
частинок, … , у ![]() -ту —
-ту — ![]() частинок;
частинок;
![]() — у
— у ![]() фіксованих ячейках розмістилися
фіксованих ячейках розмістилися ![]() частинок (
частинок (![]() ), інші
частинки розмістилися по всіх інших
), інші
частинки розмістилися по всіх інших ![]() ячейках.
ячейках.
Розв’язок
Відмітимо, що події задачі 4.2 тіж самі, що і події задачі 4.1. Але в цій задачі мова йде про розрізнимі частинки. Вважається, що всі вони різні, наприклад, кожна з них має свій індивідуальний номер.
Спосіб 1
Шукаємо ![]() — можливе число
розподілів частинок по ячейках. Для цього як і при розв’язку задачі 4.1. Випишемо
кілька можливих розподілів. Наприклад,
— можливе число
розподілів частинок по ячейках. Для цього як і при розв’язку задачі 4.1. Випишемо
кілька можливих розподілів. Наприклад,
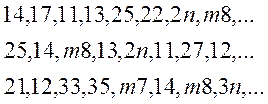
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
Тут у кожному рядку по ![]() чисел.
Перша цифра у числі – номер ячейки (тип елемента), друга цифра – номер частинки
(номер елемента). Три крапки заміняють однакові частини розподілів. Два перших
розподіли однакові за складом типів елементів, але різні за порядком
розташування номерів елементів (фрагменти
чисел.
Перша цифра у числі – номер ячейки (тип елемента), друга цифра – номер частинки
(номер елемента). Три крапки заміняють однакові частини розподілів. Два перших
розподіли однакові за складом типів елементів, але різні за порядком
розташування номерів елементів (фрагменти ![]() у
першому розподілі ,
у
першому розподілі , ![]() у другому розподілі). Третій
розподіл відрізняється від двох перших складом типів елементів і порядком
розташування номерів елементів. Отже все це різні розподіли. На відміну від
задачі 4.1 тут важче зрозуміти, які це комбінації елементів, тому почнемо з
того, що знайдемо їх кількість.
у другому розподілі). Третій
розподіл відрізняється від двох перших складом типів елементів і порядком
розташування номерів елементів. Отже все це різні розподіли. На відміну від
задачі 4.1 тут важче зрозуміти, які це комбінації елементів, тому почнемо з
того, що знайдемо їх кількість.
Частинка з номером 1 може попасти у будь-яку з т ячейок, тобто для частинки з номером 1 є т варіантів розподілу по ячейках, частинка з номером 2 – теж у будь-яку з т ячейок, …, частинка з номером n знову ж таки у будь-яку з т ячейок. Отже можливе число розподілів по ячейках
![]() ,
,
тобто виписані вище комбінації – розміщення з т елементів по n елементів з повтореннями.
1 Знайдемо тепер ![]() число розподілів частинок по ячейках, які
сприяють події А.
число розподілів частинок по ячейках, які
сприяють події А.
Нехай
![]() — ячейка номер “
— ячейка номер “![]() ” пуста
” пуста ![]() . Тоді
подію А можна подати в виді
. Тоді
подію А можна подати в виді
![]() ,
,
де ![]() — принаймні одна ячейка
пуста.
— принаймні одна ячейка
пуста.
Оскільки події ![]() сумісні,
то
сумісні,
то
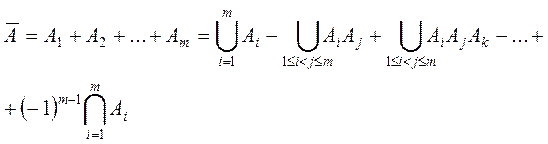
![]()
Тоді число наслідків, які сприяють події ![]()
![]()
![]()
і, відповідно, число наслідків які сприяють події А
![]()
![]()
![]()
Отже
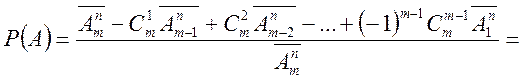
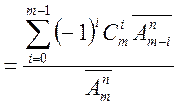
2 Знайдемо ![]() . Подію В можна подати в виді
. Подію В можна подати в виді
![]() ,
,
де ![]() — у ячейку з номером і
попало
— у ячейку з номером і
попало ![]() частинок
частинок ![]() .
.
Тоді
![]() ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.