Приклади розв’язування деяких задач (Виразити складні події через елементарні події. Знайти всі додаткові умови відносно випадкових подій для запропонованої рівності), страница 3

3          Для запропонованої рівності, яка насправді не виконується, знайти всі додаткові умови відносно випадкових подій А,В,С  і подій  і(або)  з яких би ця рівність випливала і які не зменшують область правильності рівності .

Зауваження

 Задачу розв’язати двома способами: із використан­ням таблиць істинності і шляхом еквівалентних перетворень ви­разів.

3.1      

Розв’язок

Оскільки перший спосіб розв’язання задачі вже роз­глянуто при розв’язанні задачі 2 розглянемо тут лише другий спосіб. Маємо

1)        

2)

Отже вихідна рівність еквівалентна таки рівності

За умовою задачі нам потрібно знайти всі додаткові умови відносно випадкових подій  і подій  і (або)  з яких би запропонована рівність випливала. Ясна, що більш загальна форма такої додаткової умови, яка має обмежувати (зменшувати) область визначення запропонованої рівності має бути такою

тобто вона має виключати одну з трійок подій з восьми можливих:

    

які власне задають (або утворюють) область визначення запропонованої рівності обидві частини якої задано операціями над  випадковими подіями  . Отже знайти найбільш загальні форми додаткових умов можна множенням (або множеннями) з набору. Маємо так

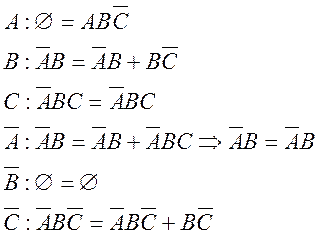
т. ч. множення на  дано нам умову

 

множення  на  нічого не дало (оскільки з тотожності ніякими множеннями більше нічого не дістанеш) і множення  на  дано нам рівнвсть з якої, помноживши її на , дістанемо ту ж саму додаткову умову    .

Зазначимо, що умова  це та умова яку дає нам помічений знаком “—” рядок таблиці істинності (див.2.1.).

Умова   породжує набір умов

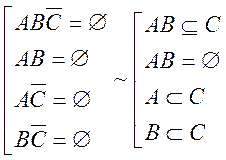
На відміну від першої додаткової умови три останніх можуть зменшувати область правильності рівності, оскільки кожна з них виключає по дві трійки подій з . Щоби розібратися із цим питанням помножимо події які утворюють (або входять в) ці умови на рівність який вони мають задовольняти. Маємо

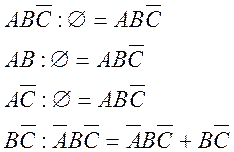
З результатів множення випливає, що умова  перетворює рівність  і її еквівалентну вихідну рівність у тотожність , із зменшенням області правильності рівності, оскільки подія  входить в однакові доданки зліва і справа від знака  „=” отриманої рівності, і отже умові задачі задовольняє. 

Відповідь: 

Зауваження

Зазначимо, що потрібну нам інформацію з  можна дістати із меншими затратами, якщо замість множення  на події з набору скористатися тим, що при ,  Дійсно, з  у даному разі маємо

Звідки  .

3.2      

Розв’язок

1)        

2)        

Отже 

Скористаємося зауваженням після 3.1.

Маємо

Звідки  або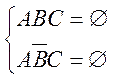    

Зазначимо, що саме ці дві умови дають нам помічені знаком “—” рядки таблиці істинності (див.2.2).

Знайдені додаткові умови породжують таку систему умов

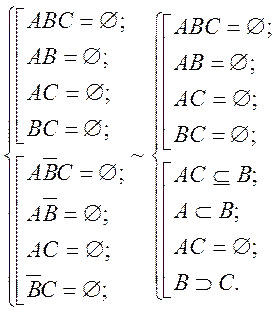
Щоби вияснити які з них зменшують область правильності рівності. Помножимо події які утворюють ці умови на .

Маємо

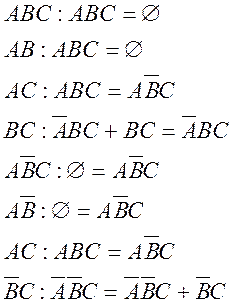
Результати множення означають, що умови  і перетворюють рівність  і еквівалентну їх вихідну рівність у тотожність  із зменшенням області правильності рівності, оскільки події  і  входять в область правильності отриманих рівностей. Отже ці дві умови із системи додаткових умов виключаємо. Система, що залишилась

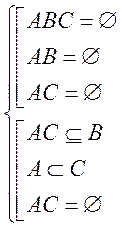
Еквівалентна дев’яти системам додаткових умов, які перевіряють на приречливість додаткових умов в них (див.2.2.) і записують відповідь.

Відповідь:

3.3      

Розв’язок

1-й спосіб.