Приклади розв’язування деяких задач (Виразити складні події через елементарні події. Знайти всі додаткові умови відносно випадкових подій для запропонованої рівності), страница 4

	+	+	+	—	+	—	—	+	—
	+	—	+	+	—	+	—	+	—
+	—	+	+	—	—	+	+	+	+
+	—	—	+	+	—	+	+	+	+
	+	+	—	—	+	—	—	+	—
	+	—	—	+	—	+	—	+	—
+	—	+	—	—	—	+	+	+	+
—	—	—	—	+	—	+	+	—	—
							*		*

Рядок помічений знаком “—” умову  яка еквівалентна набору умов

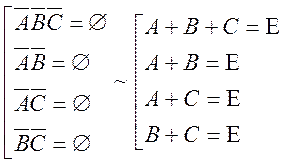
Крім рядка 8. Умова  виключає і рядок 4, а умова - і рядок 7,  що ?. Тобто умові задачі відповідають лише додаткові умови:

2-й спосіб.

1) 

2) 

Отже вихідна рівність еквівалентна рівності

  (А)

Скористаємося тим, що при  Маємо

Звідки  або

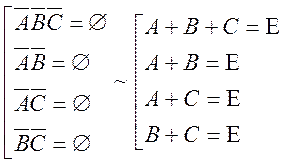
Помножимо кожну з подій, що утворюють ці умови, та (А). Маємо

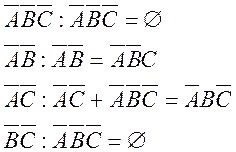
Звідки умові задачі відповідають лише додаткові умови  і оскільки події  і  не перетворюють рівність (А) у рівність з якої отримано їм відповідні умови.

Відповідь: , .

4          n нерозрізнимих частинок розподіляються по  ячейках  (статистика Бозе-Ейнштейна , якій підкоряються фо­тони, атомні ядра, атоми які складаються з парного числа ча­стинок) знайти ймовірності подій:

4.1 А – у кожній з ячейок є хоча б одна частинка;

 В – у першу ячейку попало n₁ частинок, у другу – n₂ частинок, …, у -ту – n_m частинок;

С – у l фіксованих ячейках  розподілилося  частинок(k< l) інші частинки розподілилися по всіх інших m –  ячейках.

Розв’язок

Спосіб 1

Знайдемо спочатку  — можливе чи­сло розподілів частинок по ячейках. Для цього випишимо кілька можливих варіантів розподілів. Наприклад,

	1,1,1,1	2,2,2		…	m
	1,1,1,1	2,2,2		…	m
	1,1	2	3,3,3	…	m, т

Тут у кожному рядку по n чисел, номери т ячейок, і три крапки заміняють однакові набори чисел. Оскільки частинки нерозрізнимі  то два перших розподіли однакові тому, що у під­сумку в обох випадках у кожній з ячейок розміститься однакова (для цих розподілів) кількість нерозрізнимих частинок, що до­бре видно на рис. справа, де зафіксовано остаточний ре­зультат розподілу частинок по ячейках. Третій розподіл відріз­няється від двох перших. По суті це сполучення з т типів еле­ментів по n елементів, тобто сполучення з т елементів по n еле­ментів з повтореннями. Т.ч.

1 Знайдемо тепер т_А – число розподілів частинок по ячейках, які сприяють події А. Це розподіли виду

Тут спочатку номери йдуть підряд, від 1 до т, а далі може бути будь-яка послідовність з  n — т чисел, номерів т ячейок. Тобто в кожному з них хоча б по одному разу присутні всі номери яче­йок. Тому подію А можна подати у виді

,

де  - у кожній ячейці міститься рівно по одній частинці.  - у т ячейках розподіляються будь-яким способом інші n — т час­тинок. Тоді

Отже 

 

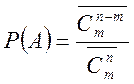
2 Оскільки частинки нерозрізнимі то події В сприяє лише один розподіл, отже

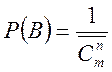
3 Подію С можна подати у виді

,

де  — у  фіксованих ячейках розподілилося  частинок ;  — у всіх інших  ячейках розподілилося  ча­стинок.