![]()
![]()
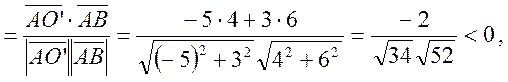
дуга кола пряму![]() не
перетинає.
не
перетинає.
Зображуємо область ![]() на
площені
на
площені ![]()
У відповідності із формулою геометричної ймовірності
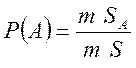
де т – площа, у даному разі. Шукаємо ![]() і
і ![]()
![]() сегмента
сегмента ![]()
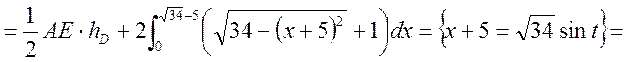
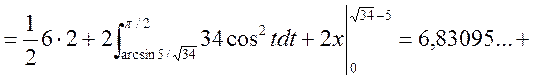
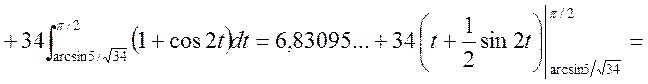
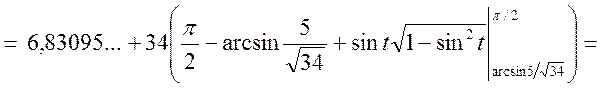
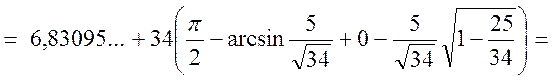
![]()
![]()
Отже 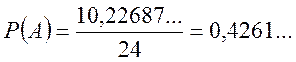
Відповідь:
![]()
6.2 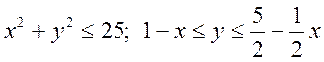
Розв’язок
Область ![]() , задана нерівністю
, задана нерівністю
![]()
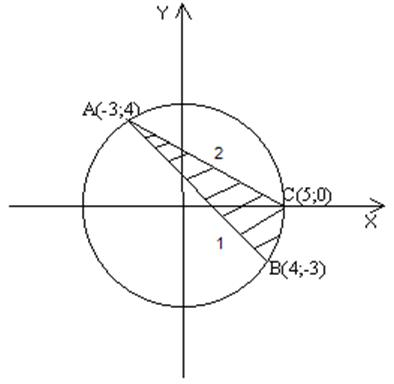
є круг, обмежений колом радіуса 5 із центром у
початку координат. Підобласть ![]() , області
, області ![]() , задана подвійною нерівністю
, задана подвійною нерівністю
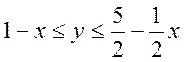 ,
,
це розміщена в середині круга область між прямими
1 ![]() і 2
і 2 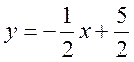 .
.
Прямі на площині ![]() визначаємо
точками перетину із колом, що обмежує область
визначаємо
точками перетину із колом, що обмежує область ![]() . Ці
точки знаходимо як розв’язки наступних систем рівнянь:
. Ці
точки знаходимо як розв’язки наступних систем рівнянь:
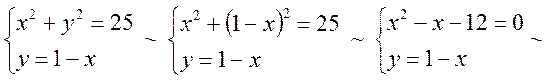
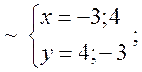
![]()
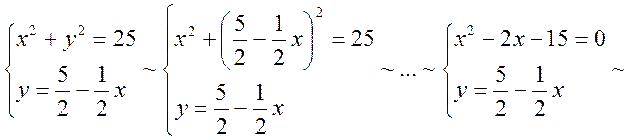
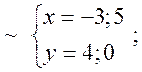
![]()
Зображуємо області ![]() і
і ![]() на площині
на площині ![]() .
.
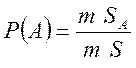
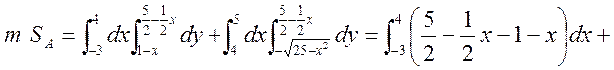
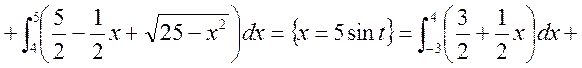
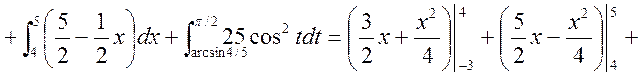
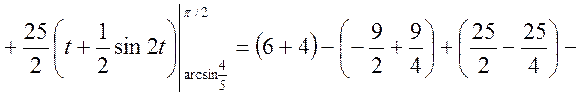
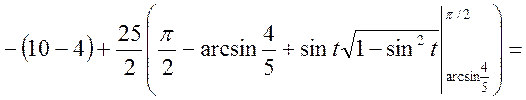
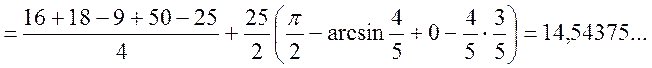
![]()
Отже
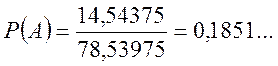
Відповідь: ![]()
7 На заданому проміжку навмання вибрано точку ![]() .
Знайти ймовірність того, що вона задовольняє вказаній умові
.
Знайти ймовірність того, що вона задовольняє вказаній умові
7.1 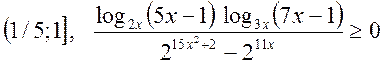
Розв’язок
Спосіб 1.
Вихідна умова
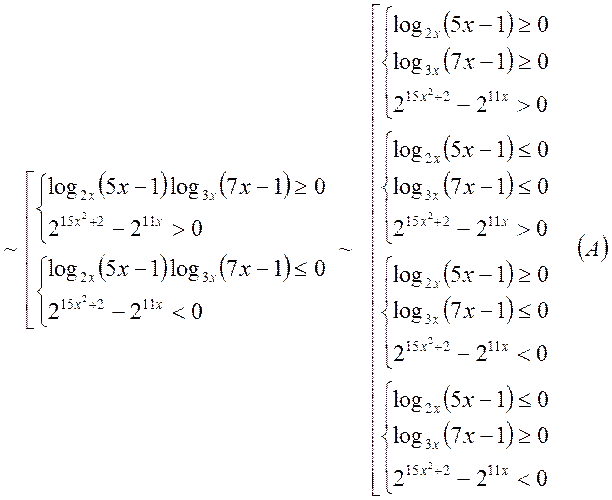
Розглянемо спочатку окремі складові умови ![]()
1) ![]()
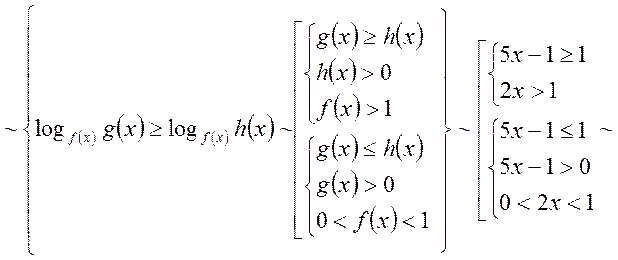
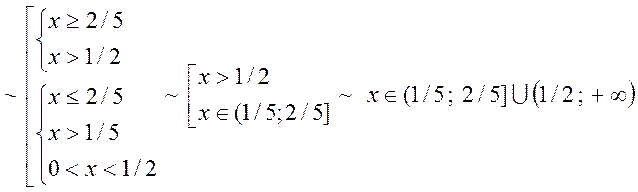
Аналогічно
2) ![]()
3) ![]()
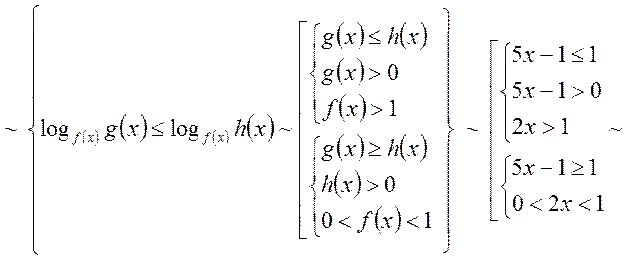
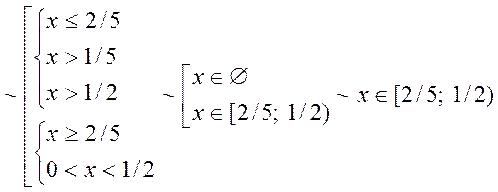
Аналогічно
4) ![]()
Відмітимо, що взагалі-то результати 3) і 4) випливають з 1) і 2).
5) ![]()
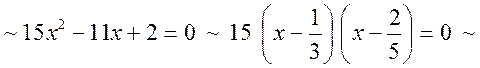
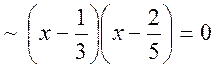
тоді умова ![]()
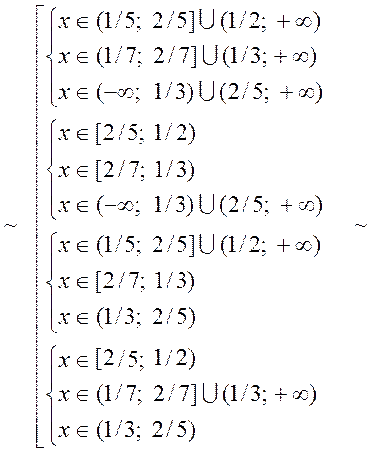
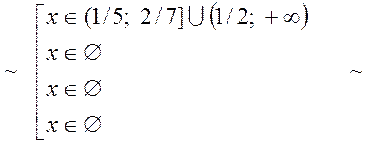
![]()
Тоді ймовірність того, що точка ![]() , навмання вибрана з проміжку
, навмання вибрана з проміжку ![]() , задовольняє заданій умові у відповідності
із формулою геометричної ймовірності
, задовольняє заданій умові у відповідності
із формулою геометричної ймовірності
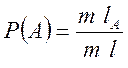 ,
,
де т довжина, дорівнює
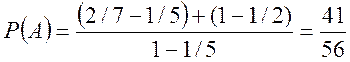
Спосіб 2.
![]() при
при ![]() або при
або при ![]()
і ![]() при
при ![]() або при
або при ![]()
Отже, при ![]() вирази
вирази
![]() і
і ![]()
мають один знак.
Вираз ![]() при
при ![]() має той же знак, що
має той же знак, що ![]() , і протилежний, якщо
, і протилежний, якщо ![]() .
.
Отже, при ![]() вирази
вирази
![]() і
і ![]()
мають один знак.
Тому задана нерівність при 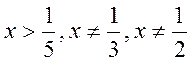
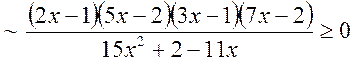
Розклавши на множники знаменник і повиносивши відмінні від нуля константи із чисельника і знаменника отримаємо
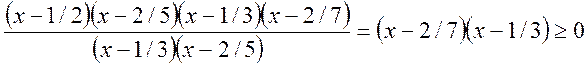 .
.
Звідки
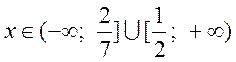 .
.
Або з урахуванням ОДЗ
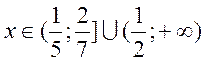 .
.
Тоді
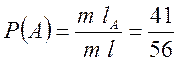 .
.
Відповідь:
![]() .
.
10 Є два слова. З першого навмання вибирають т букв, з другого – n букв. Знайти ймовірності того, що серед вибраних букв: 1) принаймні одна голосна;
2) дві однакові;
3) принаймні дві однакові;
4) усі різні;
5) одна “н”;
6) одна “н” і одна “а”;
7) одна “н” або одна “а”;(сума подій)
8) жодної “н” і жодної “а”;
9) принаймні одна “н”;
10) принаймні одна “н” і одна “а”;
11) принаймні одна “н” і принаймні одна “а”.
Зауваження
Для студентів заочного відділення у непарних
варіантах ![]() у парних
у парних ![]() .
.
10.1 Множина замкнена.
Розв’язок
Для зручності випишемо букви, з яких складаються слова, в алфавітному порядку
а ж и м н н о – 7 а а е з к м н н – 8
Нехай ![]() —
у випробуванні вибрано голосну букву і нехай
—
у випробуванні вибрано голосну букву і нехай ![]() —
подія номер
—
подія номер ![]() з умови задачі. Тоді
з умови задачі. Тоді
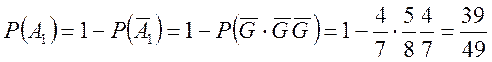
При обчисленні ймовірності ![]() враховано,
що події
враховано,
що події ![]() — у першому і другому випробуваннях,
із другого слова вибрано приголосні букви, – залежні.
— у першому і другому випробуваннях,
із другого слова вибрано приголосні букви, – залежні.
Зазначимо, що в теорії ймовірностей випадкові події, як правило, позначають великими буквами латинського алфавіту, але в межах цієї задачі задля зручності ми відмовимося від цього правила.[*]
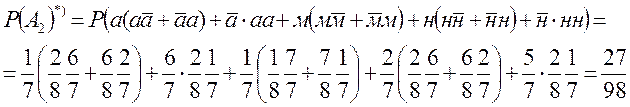
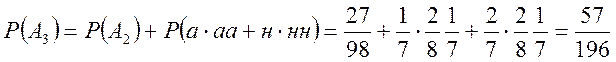
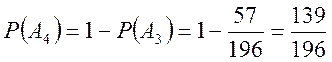
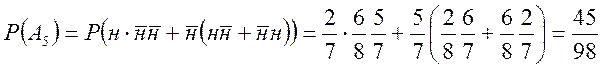
Нехай
![]() ,
,
відповідно,
![]() .
.
Тоді
![]()
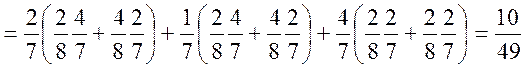
![]()
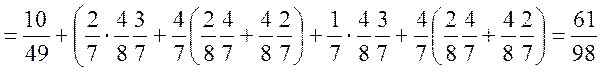
або за фомулою ![]()
![]()
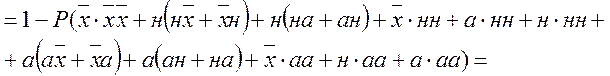
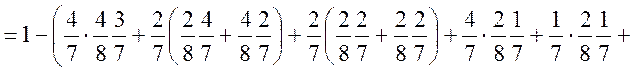
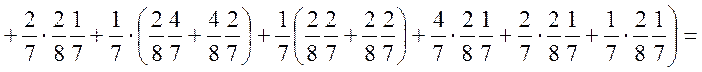
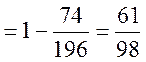
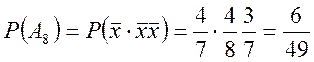
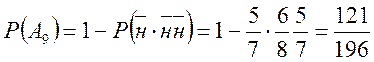
Або
![]()
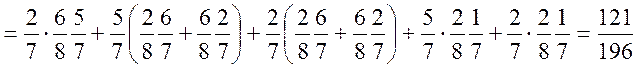
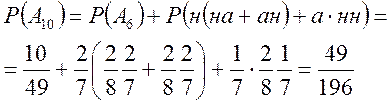
Або
![]()
Тоді у відповідності із останньою формулою
![]()
де ![]() — серед вибраних букв
одна ”а”;
— серед вибраних букв
одна ”а”; ![]() — серед вибраних букв жодної “н” і не одна
“а”.
— серед вибраних букв жодної “н” і не одна
“а”.
Отже
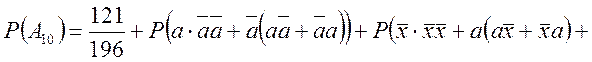
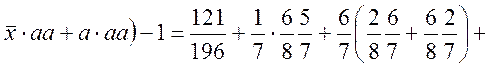
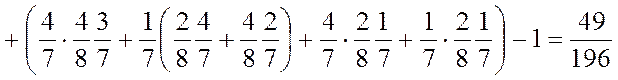
![]()
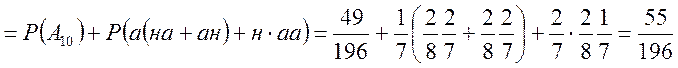
Або ![]() можна знайти іще таким
способом. Нехай
можна знайти іще таким
способом. Нехай ![]() — серед вибраних букв принаймні
одна “а”
— серед вибраних букв принаймні
одна “а”
![]()
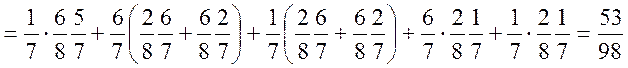
Тоді
![]()
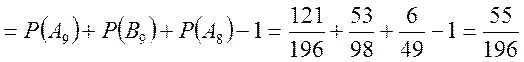
Відповідь:
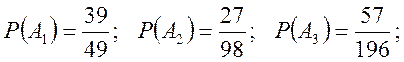
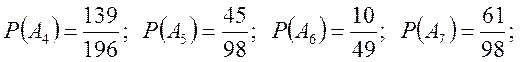
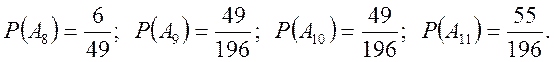
Зауваження 1
Усі знайдені вище ймовірності подій можна було б знайти використовуючи формулу
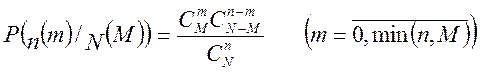
(див. зауваження в кінці розв’язку задачі 5.1).
Так
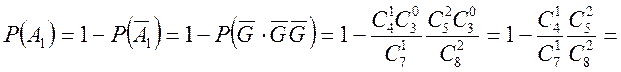
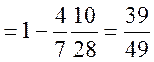
![]()
Тут і нижче множники типу ![]() рівні
1 при спрощенні виразу опускаємо
рівні
1 при спрощенні виразу опускаємо
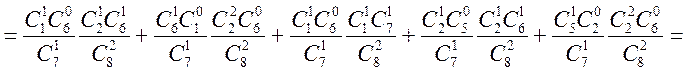
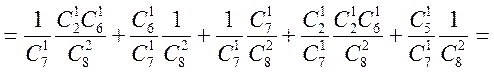
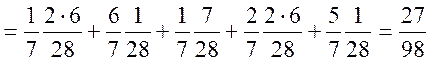
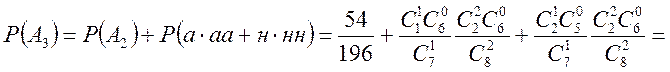
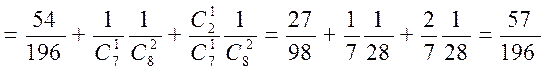
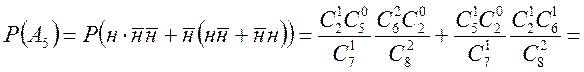
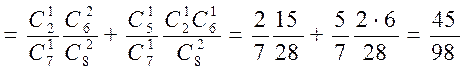
![]()
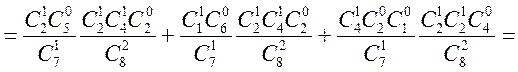
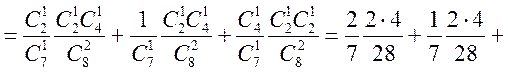
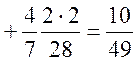
Тут ![]() , тобто не “н” і не “а”.
, тобто не “н” і не “а”.
І т.д.
Зауваження 2
У разі якщо ![]() при
обчисленні ймовірностей
при
обчисленні ймовірностей ![]() ,
, ![]() ,
, ![]() потрібно
враховувати наслідки випробування в яких є по дві пари однакових букв. Тоді
потрібно
враховувати наслідки випробування в яких є по дві пари однакових букв. Тоді
![]()
![]()
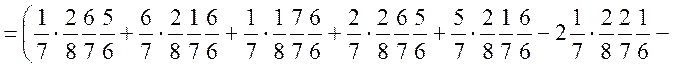
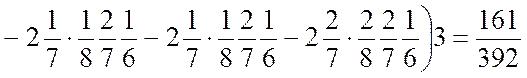
Зазначимо, що двійки перед подіями із знаком ”—”
означають, що кожна з них входить у подію із знаком ”+” двічі.
Наприклад, подія ![]() входить у події
входить у події ![]() і
і ![]() , подія
, подія ![]() у події
у події ![]() і
і ![]() і т.д.
і т.д.
![]()
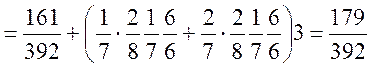
![]()
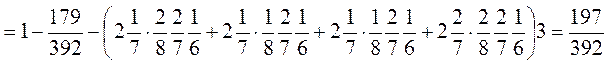
[*]) Див. зауваження 2 в кінці розв’язку задачі 10
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.