Класифікаційна настроювання електронного мікроскопа: Інформаційне і програмне забезпечення системи автофокусування електронного мікроскопу, страница 7

       Визначення 2.2.2. Множина класів розпізнавання    , , яка  відбиває  властивості скінченої множини можливих функціональних станів і відношень міх елементами системи називається абеткою (бібліотекою) класів розпізнавання.

       Множина  є простором представників, елемент якого    може служити представником класу елементів, якщо  ввести  міру схожості        d(x, )   між об'єктом     і представником .                                          

       Оцінкою властивостей ОКУ є вихідні дані, які в класифікаційному аналізі даних [    ] подаються звично в числовій формі у вигляді  матриці “об’єкт - властивість”:

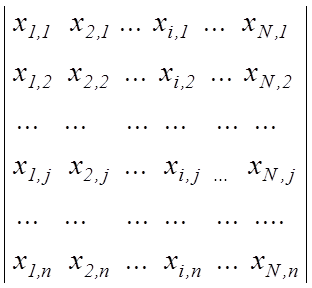                                       .                            (2.2.1)

        Формування шкірного рядка  матриці  (2.2.1) за МФСВ відбувається в процесі функціонально-статистичних випробувань      

 Визначення 2.2.3.  Функціонально-статистичними випробуваннями в МФСВ називаються природні, імітаційні або проведені безпосередньо при  функціонуванні ОКУ випробування за схемою Бернуллі, у процесі яких здійснюється оцінка інформаційної здатності СППР і приймається рішення про достатність їх проведення.

      Надалі під випробуваннями маються на увазі саме функціонально-статистичні випробування.

      Детерміновано-статистичний підхід до моделювання систем вимагає задання систем нормованих (експлуатаційних) і контрольних допусків на ознаки розпізнавання. Нехай  - клас, який характеризує максимальну функціональну ефективність СППР, тобто є найбільш бажаним для розробника інформаційного забезпечення системи.

Визначення 2.2.4.  Нормованим  називається поле допусків  {d_н,i},              i =  ,  у якому значення  і -ої ознаки розпізнавання знаходиться достовірно, тобто з імовірністю  р_і =1 або    p_i  = 0,  при    умові, що функціональний стан ОКУ  відноситься до  класу  . 

  Визначення 2.2.5.  Контрольним називається поле допусків    {d_до,і},            i = ,  на ознаки розпізнавання,  у якому значення  і -ої  ознаки розпізнавання знаходиться з імовірністю  0 < р_і < 1  при умові, що функціональний стан ОКУ  відноситься до класу  .

            У МФСВ система контрольних допусків уводитися з метою рандомізації процесу прийняття рішень, оскільки для повного дослідження ОКУ необхідно використовувати як детерміновані, так і статистичні характеристики. Зрозуміло, що  |δ_до,і |  |δ_н,і | і  система контрольних допусків (СКД) є сталою для всієї абетки класів розпізнавання.

  Визначення 2.2.6.  Реалізацією образу   називається випадковий впорядкований бінарний вектор

                      ,  j = , m = ,      (2.2.2)      

де   - і – та координата вектора, яка приймає одиничне значення, якщо значення і -ої ознаки розпізнавання знаходиться в контрольному полі допусків δ_до,і, і нульове значення, якщо  - не знаходиться;

n_min  - мінімальна кількість випробувань, яка забезпечує репрезентативність реалізацій образу.

          Отже, реалізації образу є рядками матриці (2.2.1). 

 При обгрунтуванні гіпотези компактності (чіткої або нечіткої) реалізацій образу за геометричний центр класу     приймається вершина еталонного бінарного вектора    х_m . 

Визначення 2.2.7.  Еталонний вектор   x_m - це математичне сподівання реалізацій  класу  . Він подається у вигляді детермінованого впорядкованого бінарного  вектора

                          x_m = <x_m,1 , …, x_m,і , …, x_m,N >,   m = ,               

де    х_m,і  - і -та координата вектора, яка приймає одиничне значення, якщо значення  і -ої ознаки розпізнавання знаходиться в нормованому полі допусків  δ_н,і , і  нульове значення, якщо  - не знаходиться.

  У загальному випадку процес прийняття рішень (класифікація) складається, як це було доведений експерементально  фізіологом Анохіним П.К. [  ], з двох етапів: навчання (самонавчання) і безпосереднього розпізнавання (екзамену).