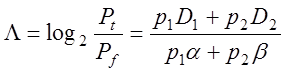 , (3.2.1)
, (3.2.1)
де ![]() -повні ймовірності правильного і неправильного прийняття
рішень відповідно;
-повні ймовірності правильного і неправильного прийняття
рішень відповідно; ![]() - апріорні ймовірності появи
відповідних подій;
- апріорні ймовірності появи
відповідних подій; ![]() - точнісні характеристики: помилки
першого та іншого роду, перша та друга достовірності відповідно. При допущенні,
що
- точнісні характеристики: помилки
першого та іншого роду, перша та друга достовірності відповідно. При допущенні,
що ![]() (найгірші в статистичному сенсі умови) міра Кульбака
набуває вигляду
(найгірші в статистичному сенсі умови) міра Кульбака
набуває вигляду
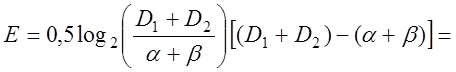
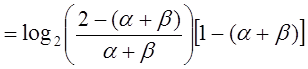 (3.2.2)
(3.2.2)
При введенні оцінок ![]() , де
, де ![]() - число реалізацій класів
- число реалізацій класів ![]() і
і ![]() відповідно, які не знаходяться в
області своїх класів;
відповідно, які не знаходяться в
області своїх класів; ![]() - кількість спостережень, які
забезпечують репрезентативність вибіркової послідовності. Тоді формула (3.2.2)
набуває робочого вигляду
- кількість спостережень, які
забезпечують репрезентативність вибіркової послідовності. Тоді формула (3.2.2)
набуває робочого вигляду
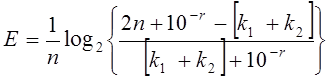
![]() (3.2.3)
(3.2.3)
де ![]() -число цифр у мантисі значення критерію
-число цифр у мантисі значення критерію ![]() , яку вводитися на випадок появи нульових емпіричних частот.
У якості розділяючої гіперповерхні (РГП) у першому наближенні береться
гіперсфера, центром якої є еталонний вектор (ЕВ)
, яку вводитися на випадок появи нульових емпіричних частот.
У якості розділяючої гіперповерхні (РГП) у першому наближенні береться
гіперсфера, центром якої є еталонний вектор (ЕВ) ![]() .
.
Оскільки сучасні ЕОМ
дозволяють розрізняти 256 градацій чорно-білого зображення, те його обробку
доцільно здійснювати шляхом сканування рецепторного полючи, що є природним для
РЕМ, і побудови розподілу яскравості для шкірного рядка рецепторів. Квантовані
в часі криві розподілів яскравості розглядаються як випадкові реалізації
зображення ![]() , де
, де ![]() ;
; ![]() - змінна числа рецепторів у рядку.
- змінна числа рецепторів у рядку.
З метою формування бітового
масиву значень реалізацій ![]() здійснюється їх квантування
на два рівні за формулою
здійснюється їх квантування
на два рівні за формулою
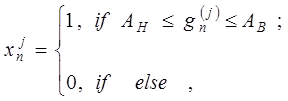 (3.2.4)
(3.2.4)
де ![]() - нижній і верхній контрольний допуски на рецептори.
Оптимізація контрольних допусків в інформаційному сенсі здійснюється
безпосередньо в рамках алгоритму КН. За початкові значення
- нижній і верхній контрольний допуски на рецептори.
Оптимізація контрольних допусків в інформаційному сенсі здійснюється
безпосередньо в рамках алгоритму КН. За початкові значення ![]() і
і ![]() приймаються відповідно
приймаються відповідно ![]() і
і ![]() , де
, де ![]() - номінальне (середнє) значення яскравості зображення.
Оскільки двобічне поле контрольних допусків вибрано симетричним, те початкове
значення
- номінальне (середнє) значення яскравості зображення.
Оскільки двобічне поле контрольних допусків вибрано симетричним, те початкове
значення ![]() дорівнює чверті шкали яскравості,
тобто 64. Формування бінарного ЕВ базового класу
дорівнює чверті шкали яскравості,
тобто 64. Формування бінарного ЕВ базового класу ![]() здійснюється за формулою
здійснюється за формулою
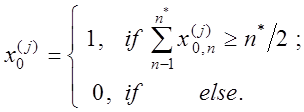 (3.2.5)
(3.2.5)
Аналогічно обробляється
поточне зображення ![]() . Отже, у процесі обробки зображень
. Отже, у процесі обробки зображень ![]() і
і ![]() здійснюється формування вхідних
даних, які за МФСВ необхідні для обчислення інформаційної міри між базовим і
поточним зображеннями. Такими вхідними даними є ЕВ
здійснюється формування вхідних
даних, які за МФСВ необхідні для обчислення інформаційної міри між базовим і
поточним зображеннями. Такими вхідними даними є ЕВ ![]() і відповідно випадкові реалізації
і відповідно випадкові реалізації ![]() ,
, ![]() .
.
Визначення
оптимальної в інформаційному сенсі кодової відстані ![]() - радіуса
РГП, здійснюється за послідовним алгоритмом
- радіуса
РГП, здійснюється за послідовним алгоритмом
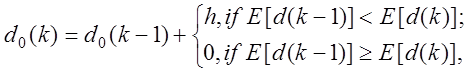 де k – число прирощень
радіуса; h – крок прирощення. Обчислення КФЕ закінчується при знаходженні
екстремального значення
де k – число прирощень
радіуса; h – крок прирощення. Обчислення КФЕ закінчується при знаходженні
екстремального значення 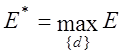 , де
, де ![]() –
множина радіусів РГП класу
–
множина радіусів РГП класу ![]() ;
; ![]() -
міжцентрова кодова відстань.
-
міжцентрова кодова відстань.
Оптимізація контрольних допусків
здійснюється після вибору ![]() для базового класу
для базового класу ![]() , за алгоритмом
, за алгоритмом ![]() , якщо
, якщо 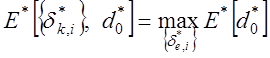 , де
, де ![]() – система нормованих полів допусків на
рецептори.
– система нормованих полів допусків на
рецептори.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.