Класифікаційна настроювання електронного мікроскопа: Інформаційне і програмне забезпечення системи автофокусування електронного мікроскопу, страница 5

На фокусування зображення впливають різні параметри.

Їхньої назви, також межі регулювання приведені в таблиці 1.2.2.

Однак на практиці, при фокусуванні об'єкта, основним змінюваним параметром є только струм фокусирующей лінзи.

1.3 Постановка задачі дослідження

Автоматизація настроювання складних систем контролю і керування в даний час залишається усе ще однієї з важко формалізованих задач. Визначену надію на її рішення зв'язують з інтенсивною розробкою методів автоматичної класифікації.

Розглянемо постановку задачі автонастройки в рамках методу функціонально-статистичних іспитів, що базується на оцінці інформаційної здатності системи автоматичної класифікації. Нехай - клас настроювання, що характеризує найбільшу функціональну ефективність Е_max  системи. Дано вектор параметрів настроювання g = <g₁,..,g>, де L число параметрів  і відомі відповідні обмеження на параметри R_i(g₁,..,g) = 0. Тоді X₀ вихідне (базове) стан не набудованого ОКУ.

Потрібно змінити параметри настроювання так, щоб при перекладі ОКУ з класу X₀ у клас   інформаційна міра Е була максимальна. При цьому розглянутий параметр на кожнім кроці настроювання n по алгоритму

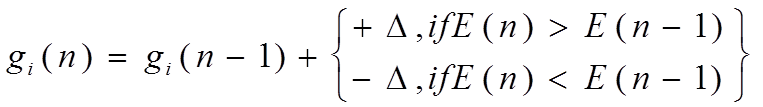
У даній дипломній роботі, виходячи з завдання, потрібно розглянути питання оцінки функціональної ефективності системи автонастройки фокусности електронного мікроскопа. Одержати математичну модель у рамках МФСИ, на підставі якої розробити алгоритм автофокусировки растрового електронного мікроскопа, що дозволяє здійснювати оперативну автофокусировку.

Розділ 2. Метод функціонально статистичних випробувань(МФСВ)

 2.1 Інформаційна модель СППР

Структурну модель СППР у загальному випадку можна податі у вигляді суперблоку, наведеного на мал. 2.1.1.  Отут вхідними даними  є: вектор-реалізація  образу , який характеризує функціональний стан ОК, вектор випадкових збурень , які контролюються, і  вектор випадкових збурень  f(t),  які не контролюються.

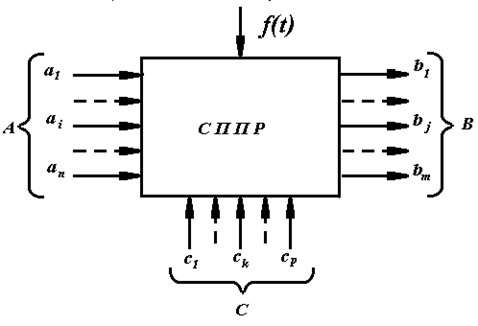
Малюнок 2.1.1

     Вихідними даними СППР є вектор  B{b_j }, який належить простору допустимих рішень   В.

     Вектор З може суттєво впливати на функціональну ефективність СППР, оскільки він може позначатися на достовірності розпізнавання, наприклад, при зміні кліматичних, вибраційних, радіаційних, фізіологічних, економічних або інших розумів здійснення процесу класифікації.

Розглянемо інформаційний опис СППР для загального випадку, тобто із урахуванням вектору З={C_p}. Кількість середньої умовної інформації про вектори А і В відносно один одного при наявності на вході вектора З дорівнює

 I_c(A, B)=H(A/C)-H(A/B, C)=H(B/C)-H(B/A, C)=I_p(B, C),              (2.1.1)

або у вигляді ймовірностей має вигляд [    ]

           *  .

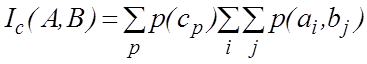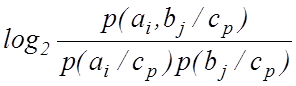     Оскільки

                                           I_A,C(B) = H(B) - H(B/A,C),                                 (2.1.2)

те віднявши від обох частин (2.1.2) відповідно I_C(B)=H(B)-H(B/C)  і  врахувавши  (2.1.1)  отримаємо

                                         I_A,C (B)= I_C (B)+ I_c (A, B).                                   (2.1.3)

       Із  (2.1.3) випливає, що

                                                I_A,C(B)³ I_C(B),                                           (2.1.4)

тобто кількість інформації, яка міститься у векторі  В  про залежні вектори  А і  С  не менше кількості інформації, яка міститься у векторі  В  про вектор  С. При цьому в (2.1.4) має місце рівність при умові, що вектори  А  і  В  незалежні, оскільки   I_A,C (B)=0   і тоді    H(A / C) = H( A /B, C).

          На практиці часто виправдано застосування інформаційної моделі СППР при умові, що вектори  А  і  С  незалежні. Тоді аналогічно (2.1.3) отримаємо вираз.

                                             I_B,C(A)=I_B(A)+I_B(A,C).                                (2.1.5)

       Із  (2.1.5) при незалежності   В   і   С  витікає

                                         I_B,C (A)=I_B (A)  і   I_B (A,C)=0.