Розіб'ємо безліч можливих щирих значень контрольованого параметра на двох областей m1 и??. Область m1 включає значення параметра, що знаходиться в допуску, а m2- не в допуску. Тоді замість (2.3.5) - (2.3.8) можна записати:
a = p(g2 /m1); b = p(g1 /m2); D1 = p(g1 /m1); D2 = p(g2 /m2); (2.3.9)
З (2.3.9) випливає для повних груп подій наступна зв'язок між точностными характеристиками:
a + D1=1; b + D2= 1; (2.3.10)
Крім того, імовірність ухвалення помилкового рішення на підставі теореми про повну імовірність дорівнює:
PОШ=p(m1)a + p(m2)b , (2.3.11)
а імовірність ухвалення правильного рішення -
PПР =p(m1)D1 + p(m2)D2 , (2.3.12)
Виразивши
апостеріорні імовірності p(gm /ml) через апріорні по формулі
Байеса: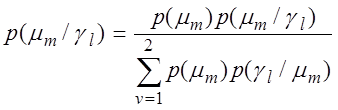 
(2.3.13)
і позначивши p(m1) = p1 і p(m2) = p2 з обліком (2.3.5) - (2.3.8) одержимо:
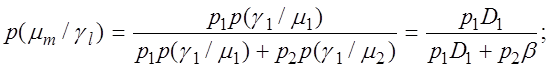
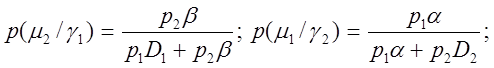
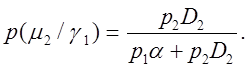(2.3.14)
Після підстановки (2.3.14) у (2.3.4) при p1= p2=0.5 одержимо формулу для обчислення кількості середньої умовної інформації з точностным характеристик СППР при двухальтернативном рішенні:
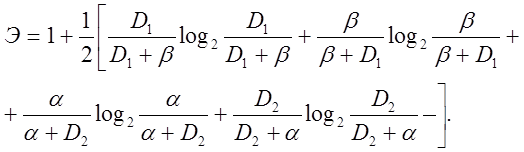(2.3.15)
У загальному випадку, що характеризує процес прийняття рішень, побудований на підставі (2.3.15) графік функції Э представляє поверхня в тривимірному просторі.
На малюнку 2.3.2 показаний перетин цієї поверхні по бісектрисі D1ОD2 кути. Крива отримана при p1=0.6 і p2 =0.4. При цьому функція Э є неоднозначної. На практиці цю неоднозначність можна обійти, обмеживши зміною достоверностей в інтервалі [0.5;1], що визначає робочу область. Як видно з малюнка 2.3.2 у робочій (заштрихованої) області кількість інформації збільшується зі збільшенням достоверностей.
|
Малюнок 2.3.2 - Перетин поверхні інформаційного критерію (D1=D2).
Саме в цій області екстремальні значення параметрів навчання, що відповідають максимуму критерію, є оптимальними в інформаційному змісті.
На практиці точностные характеристики заміняються емпіричними частотами. Для двухальтернативного рішення введемо наступні оцінки точностных характеристик:
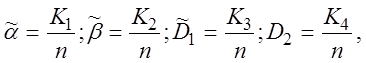(2.3.16)
де K1 і K3 число подій, що полягає в перебуванні значення параметра поза полючи допусків і в поле допусків відповідно за умови, що щире значення параметра знаходиться в поле допусків; K2 і K4 - число подій, що полягають у перебуванні обмірюваного значення параметра в поле допусків і поза полючи допусків відповідно за умови, що щире значення параметра знаходиться поза полючи допусків; n - число іспитів. На підставі (2.3.15) з обліком (2.3.16) формула (2.3.4) прийме вид:
ЭI=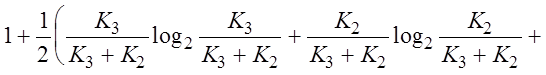
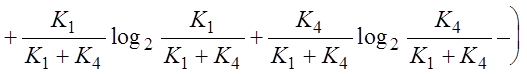. (2.3.17)
Таким чином, інформаційний критерій (2.3.17), будучи функціоналом точностных характеристик, прямо характеризує ефективність функціонування СППР у залежності від перебування контрольованих параметрів (ознак) у своїх експлуатаційних і контрольних допусках.
Для перебування максимального значення критерію Э, будується гіперсфера з центром у вершині еталонного вектора для поточного класу, радіус d якої збільшується від 0 доти, поки поточне значення Э, не стане менше його попереднього значення. Для кожного значення d обчислюється відстань (шляхом додавання по модулі 2) між еталонним вектором і кожною реалізацією для поточного класу, а також для класу, найближчого до поточного. У залежності від значення кодової відстані, одержує збільшення один з коефіцієнтів ДО1, ДО2, ДО3, K4 (для найближчого до поточного класу). Після визначення цих коефіцієнтів обчислюється Э, по формулі (2.3.17). У випадку, якщо поточне значення Э менше попереднього (Эдред), Эдред вважається максимальним значенням інформаційного критерію. У противному випадку обчислення повторюються для радіуса, збільшеного на одиницю. Значення d, що відповідає найбільшому Э, є радіусом поділяючої гіперповерхні для даного класу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
