Класифікаційна настроювання електронного мікроскопа: Інформаційне і програмне забезпечення системи автофокусування електронного мікроскопу, страница 10

-залежати від точностных характеристик СППР.

 Усім цим вимогам задовольняють критерії, що характеризують інформаційну здатність системи.

У даній роботі для автонастройки складної системи як критерій оцінки функціональної ефективності класифікації станів використовується інформаційний критерій виду :

                       Э_I =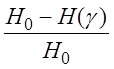 ,                                                            (2.3.1)

де                             H₀ = -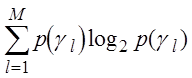                                      (2.3.2)

- апріорна (безумовна) ентропія;

  H(g)=-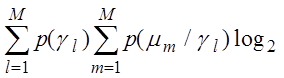 ,                                     (2.3.3)                                                                                                         

- умовна ентропія, що характеризує невизначеність ухвалення рішення, де p( g_e  ) – апріорна імовірність прийняття гіпотези, p(m_m  /  g_e) - апостеріорна умовна імовірність того, що має місце подія m_m за   умови прийняття гіпотези g_e   ;  M - число альтернативних гіпотез.

Застосування критерію (2.3.1) для оцінки ефективності функціонування складних систем представляється природним і найбільше що повно відбиває їхню інформаційну природу. 

На практиці при оцінюванні функціональної ефективності  мають місце наступні реальні допущення:

-не враховуються витрати на одержання й обробку інформації;

-рішення є двухальтернативным   (M=2);

-для реальної СППР апріорна інформація є неповної, тому виправдане прийняття равновероятных гіпотез:  p(g ₁) = p(g ₂) = 0.5;

-при кожнім іспиті здійснюється однокрокова процедура ухвалення рішення.

 Тоді критерій (2.3.1) приймає простий приватний вид:

            Э_{I 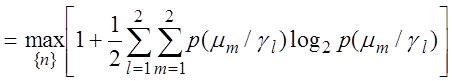,}                            (2.3.4)

Критерій (2.3.4) повною мірою задовольняє сформованим вище вимогам до КФЭ.

При двухальтернативной системі оцінок рішень, наприклад, при допусковом контролі у формі "У НОРМІ" - "НЕ В НОРМІ" як основну гіпотезу приймемо гіпотезу про перебування обмірюваного значення контрольованого параметра в поле допусків і як альтернативну гіпотезу - гіпотезу про перебування обмірюваного значення параметра не в поле допусків. При цьому, мають місце чотири можливих результати процесу контролю, що характеризуються наступними імовірностями - точностными характеристиками:

- помилка першого роду (Малюнок 2.3.1а); умовна імовірність того, що измерянное значення лежить поза полючи допуску за умови, що щире значення належить полю допуску: 

                       a = p( xÎ d / z Îd );                                                    (2.3.5)

- помилка другого роду (Малюнок 2.3.1б); умовна імовірність того, що измерянное значення лежить у поле допуску за умови, що щире значення не належить полю допуску:

                       b = p( xÎ d / z Îd );                                                    (2.3.6)

 - перша вірогідність (Малюнок 2.3.1в); умовна імовірність того, що измерянное значення лежить у поле допуску за умови, що щире значення також належить полю допуску:

                       D₁ = p( xÎ d / z Îd );                                                   (2.3.7)

- і друга вірогідність (Малюнок 2.3.1г); умовна імовірність того, що измерянное значення лежить поза полючи допуску за умови, що щире значення також не належить полю допуску:

                       D₂ = p( xÎ d / z Îd );                                                  (2.3.8)

де  x і z - відповідно обмірюване і щире значення параметра;

 d - поле допуску на значення параметра.

 

а) помилка першого роду

 б) помилка другого роду

 

в) перша вірогідність

г) друга вірогідність

Малюнок 2.3.1 – Можливі исходы при двухальтернативном рішенні.