Класифікаційна настроювання електронного мікроскопа: Інформаційне і програмне забезпечення системи автофокусування електронного мікроскопу, страница 13

Отже, вибір n_min доцільно здійснювати в компромісній області ІІ (мал.2.4.1,а) при умові відсутності викидів довірчого інтервалу до значень, близьких до нуля або одиниці. Для багатьох практичних задач значення  D  вибирається з інтервалу  [0,3;0,35].

У загальному випадку, треба будувати довірчі інтервали для всіх  N  ознак і вибирати  n_min  за умовою

              n_min=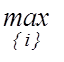(n_{min 1}, ..., n_{min i}, ..., n_{min N}).

Однак при відповідному виборі системи контрольних допусків на ознаки розпізнавання та забезпеченні розумів статистичної сталості та однорідності проведення випробувань можна вибирати n_min за довірчим інтервалом, побудованим для будь-якої однієї ознаки, що  знижує обчислювальну трудомісткість алгоритму.

Розділ 3. Інформаційне та програмне забеспечення системи автофокусування   електронного мікроскопа

        3.1 Математична модель автофокусування електронного мікроскопу

          Автоматизація настроювання складного об’єкту контролю та управління (ОКУ) усі ще залишається однією із важко формалізуємих задач. Надії на її розв'язання пов'язуються з появою робочих алгоритмів автоматичної класифікації. Розглянемо постановку та алгоритм розв'язання задачі класифікаційної настроювання (КН) у рамках методу функціонально-статистичних випробувань (МФСВ), який грунтується на оцінці інформаційної здатності системи прийняття та підтримки рішень (СППР), що навчається [1-3].

Нехай   - клас, який характеризує найвищу функціональну ефективність  системи, що настроюється. Дано вектор параметрів настроювання , відповідні обмеження на них  і клас , який характеризує початковий стан ОКУ, що настроюється. Треба в межах заданої оперативності за  кроків настроювання перевести ОКУ із класу  в клас  при умові досягнення максимального значення критерію функціональної ефективності (КФЕ) 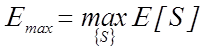 . На теоретико-множинному рівні складовою частиною математичної моделі системи КН складного ОКУ є модель інформаційної системи:

 ,                                                      (1)

де Т - множина моментів зняття інформації; W - простір ознак розпізнавання;  G, X - вхідні та вихідні змінні; Z - множина станів ОКУ;  - оператор переходів;  - оператор виходу, що формує вихідну (вибіркову) послідовність даних. У комп'ютерних СППР вибіркова множина  X  є звичайно підмножиною бінарного простору  X. Оператор   розбиває множину X на два класи: початковий , який характеризує початковий ненастроєний стани ОКУ і поточний , який характеризує стан ОКУ після реалізації потокового кроку настроювання. При цьому в МФСВ розбиття  ,  у загальному випадку, є нечітким, тобто допускає перетин класів розпізнавання і відповідає умовам:

() [ Ø];

() () [ Ø];

( )( ) [ Ø];

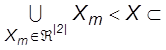 X ,  m=1, 2 ,

де   - класи розпізнавання. Оператор ₤^|1| утворює апріорне нечітке покриття ₤^|1|, яку складається з бажаного (фінішного) класу настроювання . Комутативне кільце замикає оператор æ: ₤^|1|. Оператор прийняття рішень (класифікації)   відображає розбиття  на область допустимих рішень  ,  де  m – кількість гіпотез. Шляхом оцінки прийнятих гіпотез оператор γ: Á ^|l|формує множину точнісних характеристик Á ^|l|, де l = m² – кількість точнісних характеристик. Оператор Á^|l| обчислює множину значень інформаційного КФЕ, який є функціоналом точнісних характеристик [3]. Діаграма відображень множин, задіяних при КН за МФСВ має вигляд:

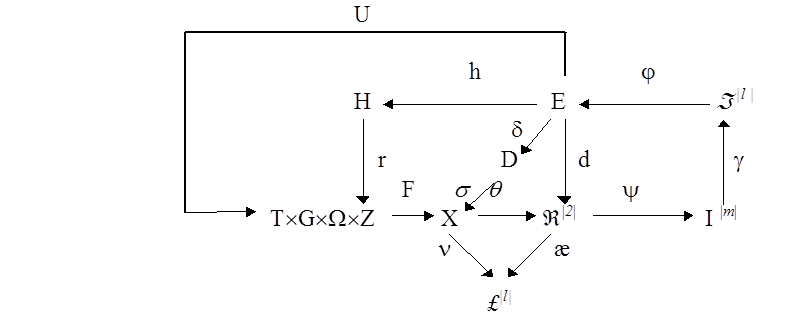                       (2)

Діаграма відображень вміщує чотири контури зворотнього зв'язку. Перший контур  здійснює оптимізацію геометричних параметрів розбиття  Â^|2|  за інформаційними КФЕ. Другий контур  оптимізує в інформаційному сенсі систему контрольних допусків  D на значення ознак розпізнавання. (ОР). Третій контур реалізує ітераційну процедуру КН шляхом пошуку максимуму критерію  Е. При цьому оператор  h:E®H відображає значення КФЕ на множину  значень параметрів настроювання, а оператор  r:H®Z   здійснює на шкірному кроці перехід ОКУ в новий клас. Оператор  U:E®T´G´W´Z - замикає зовнішній контур управління процесом КН.