Класифікаційна настроювання електронного мікроскопа: Інформаційне і програмне забезпечення системи автофокусування електронного мікроскопу, страница 12

Однак існують ситуації, у яких максимальне значення критерію є неінформативним, наприклад, перебування максимальне вилученого в інформаційному змісті  класу. У таких випадках використовується площа робочої області критерію. Алгоритм її обчислення схожий з алгоритмом перебування максимального значення з тією різницею, що виробляється підсумовування всіх значень критерію в робочій  області.

 2.4  Визначення мінімального обсягу навчальної вибірки

Навчальна вибірка має на практиці скінченну довжину  n, що обумовлює наявність статистичної похибки  e  між імовірністю  p_i  та емпіричною частотою  k_i n  знаходження значення  i -ої ознаки розпізнавання у своєму контрольному полі допусків    δ_до,і . Верхня оцінка похибки  e =|p_i - |   у залежності від кількості випробувань n визначається за теоремою Муавра-Лапласа [  ]:

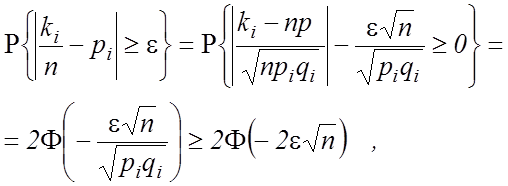(2.4.1)

де  k_i  - кількість  подій, при яких    значення  i -ої ознаки  знаходиться в полі допусків  δ_до,і ;  q_i=1-p_i - імовірність відсутності значення  i -ої  ознаки  в полі допусків;  ?(...) - функція Лапласа.

Визначення мінімальної довжини   n_min навчальної вибірки зробимо за умови отримання допустимої статистичної похибки та оперативності  алгоритму обчислення n_min . Ці вимоги є суперечливими, що обумовлює компромісний характер розв'язання цього завдання. Скористаємось методом динамічного довірчого інтервального оцінювання. Суть методу полягає в побудові після шкірного випробування довірчого інтервалу, який оцінює ймовірність р_і  знаходження i -ої ознаки в полі допусків   δ_до,і  з імовірністю  1-Q :

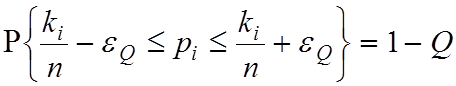.           (2.4.2)

     Визначення максимальної похибки   e_Q  у залежності від обсягу вибірки  n  при заданому рівні значущості Q здійснюється за співвідношенням

.                                (2.4.3)

 За Q вибирають бу-яку мале позитивне число (звичайно вибирають одне із значень: 0.05; 0.01; 0.001). З урахуванням властивості функції Лапласа Ф(х)=1-Ф(-х) перетворимо (2.4.3) до вигляду

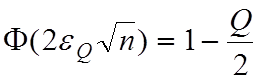.                    (2.4.4)

     Для  Q=0.05  за таблицею функції  Лапласа  ,     з урахуванням    (2.4.4) для            Ф(х)= 1 - Q/2 = 0.975, знайдемо значення аргументу . Тоді  похибка  e_Q  змінюється в залежності від довжини навчальної вибірки  n  за гіперболічним законом:

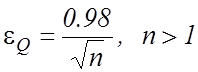.                                (2.4.5)

На мал.2.4.1,а  наведено графік  e_Q = f(n), де умовно виділено три області значень n, які відрізняються крутизною функції. Область І є забороненою областю , оскільки похибка перебільшує допустиму. Область ІІІ характеризується значними економічними втратами при малій швидкості зменшення похибки e_Q. Область ІІ є компромісною і охоплює  інтервал приблизно від 40 до 80 випробувань. Легко довести, що при різних значеннях Q графік функції  e_Q = f(n) буде переміщуватися паралельно по вертикалі, не змінюючи свого вигляду. Графічно довірчий інтервал можна створити, обчислюючи для шкірного випробування  n  за виразом (2.4.5)  похибку  e_Q  i відкладаючи її зверху та знизу від графіка частоти  k_i n. На мал.2.4.1,б зображено графік динамічного довірчого інтервалу оцінки ймовірності знаходження значення і -ої ознаки в полі допусків δ_до,і  при рівні значущості Q=0,05 у залежності від числа випробувань  n. 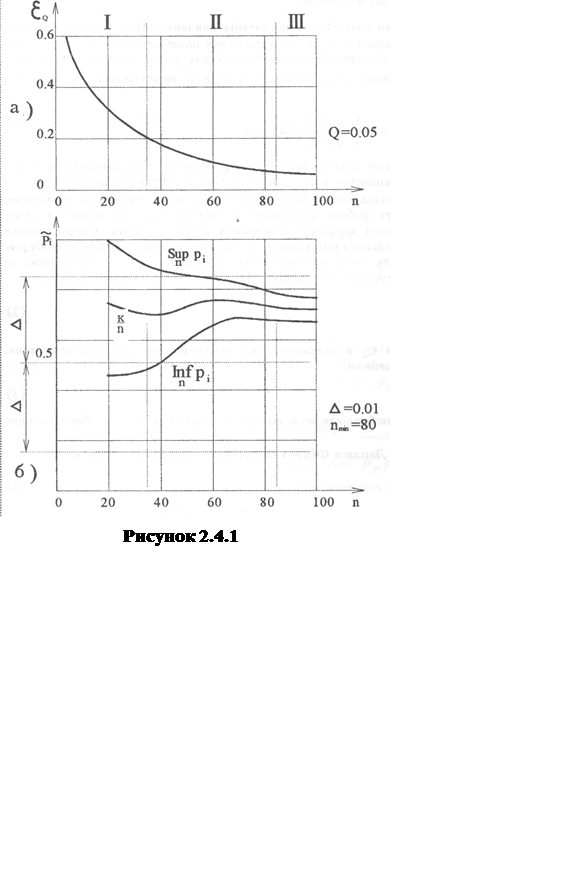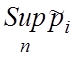При цьому  верхня  та нижня  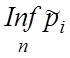межі довірчого інтервалу  при збільшенні числа вирообувань мають тенденцію до зближення з емпіричною частотою.

 Для знаходження мінімального числа випробувань n_min ,  яку гарантує прийнятні з практичних міркувань величину похибки і оперативність реалізації алгоритму обчислювання, необхідно знайти критерій зупину випробувань. Таким моментом вважається випробування, при якому поточний довірчий інтервал накривається заданим інтервалом [0,5±D], де ½D½<0,5. Останній (правий) перетин заданого інтервалу з однією з меж довірчого інтервалу визначає  випробування  n_min , яку гарантує з імовірністю 1-Q, що максимальна похибка e_Q не  перебільшує  значення функції    ε_Q =f(n)       при  n=n_min.