Электротехника \ Электротехника, электроника и микропроцессорная техника

Класифікаційна настроювання електронного мікроскопа: Інформаційне і програмне забезпечення системи автофокусування електронного мікроскопу, страница 14

У якості критерію оптимізації в МФСВ виступає інформаційний критерій, який, наприклад, за мірою Шеннона для двохальтернативної системи оцінок приймаємих рішень і для рівноймовірних гіпотез може мати вигляд 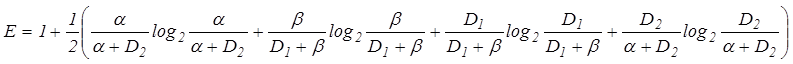[3]:

, (3)

де a,b, D₁, D₂- помилки першого та іншого роду, перша та друга достовірності відповідно. У роботі [3] розглянуто обчислювальний аспект оцінювання функціональної ефективності СППР за критерієм (3) та досліджено залежність границь робочої області його значень від точнісних характеристик.

За МФСВ алгоритм КН полягає в обчисленні на шкірному кроці настроювання інформаційної міри , яка є диференційною мірою різноманітності початкового і потокового класу , , де -екстремальний крок настроювання, порівнянні значення з попереднім і в зміні в залежності від результату порівняння значення управляючого параметру за ітераційним алгоритмом:

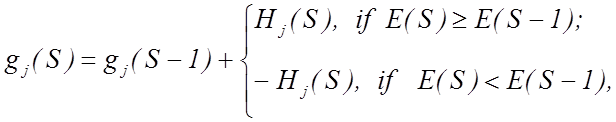(4)

де – крок зміни j-го параметра. Оцінка функціональної ефективності КН за МФСВ здійснюється в процесі навчання за алгоритмом, який визначає оптимальні в інформаційному сенсі параметри навчання, що безпосередньо впливають на ефективність настроювання [2]. Такими параметрами є радіуси розділяючих гіперсфер, які в кодовій відстані Хеммінга визначаються як 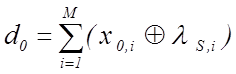, де - еталонний вектор класу ; - деяка вершина вектора-реалізації образу на гіперсфері; - кількість ОР; - операція складання за модулем 2 і система контрольних допусків на ознаки розпізнавання, яка безпосередньо формує навчальну вибірку (НВ) і впливає на значення критерію .

Розглянемо обчислення інформаційного КФЕ, наприклад, за формулою (3) у рамках алгоритму навчання за МФСВ. Оскільки кожна автоматизована система управління грунтується на допусковій концепції оцінки параметрів контролю, значення яких, у загальному випадку, можуть належати одному із трьох класів: – “НОРМА”, ^__ “МЕНШЕ НОРМИ”, - “БІЛЬШЕ НОРМИ”, те запуск алгоритму КН системи здійснюється з моменту встановлення її виходу із класу .

На підготовчому етапі (S=0) формується для класу X₀ матриця “об’єкт-властивість” де , ^__змінні кількості реалізацій образу і ОР відповідно; - мінімальний обсяг репрезентативної НВ [4]. З метою рандомізації даних задається початкова (базова) система контрольних допусків, яка складається з двох масивів : {ND[I]}, {VD[I]} масиви нижніх і верхніх допусків. Шляхом порівняння значень ОР зі своїми допусками формується бітовий масив НВ , який складається з реалізацій образу : , де

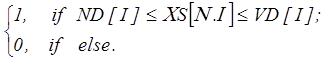
На шкірному кроці S згідно вибраним напрямку і стратегії настроювання здійснюється зміна значення параметрів {g } і формуються аналогічні матриці і для потокового класу . Шляхом статистичного усереднення НВ визначаються еталонні вектори і , які розглядаються як геометричні центри своїх класів. Для пошуку максимуму критерію E(S) за МФСВ здійснюється процедура оптимізації радіуса розділяючої гіперсфери класу за алгоритмом:

(k) = (k-1)+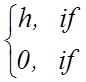

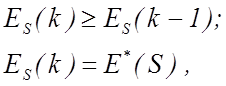
де k - число прирощень радіуса; h - крок прирощення; 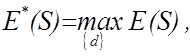де множина радіусів розділяючих гіперсфер класу .

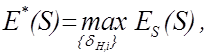Після визначення екстремального значення здійснюється оптимізація контрольних допусків за алгоритмом , якщо де система нормованих полів допусків на ОР, які визначають область значень відповідних контрольних допусків. Обчислення критерію (3) на k-му кроці навчання здійснюється шляхом оцінки точнісних характеристик: , де коефіціенти обчислюються за алгоритмом: