Конструкционная характеристика стали. Основы расчета стальных конструкций. Соединения стальных конструкций. Проектирование конструкций балочной клетки. Проектирование центрально сжатых стержней, страница 25

            Отношение расчетной длины к длине стержня называется коэффициентом приведения или коэффициентом расчетной длины – μ = l₀/l. В последовательности стержней по рис. 45 они равны – 2; 0,7; 1; 0,5.

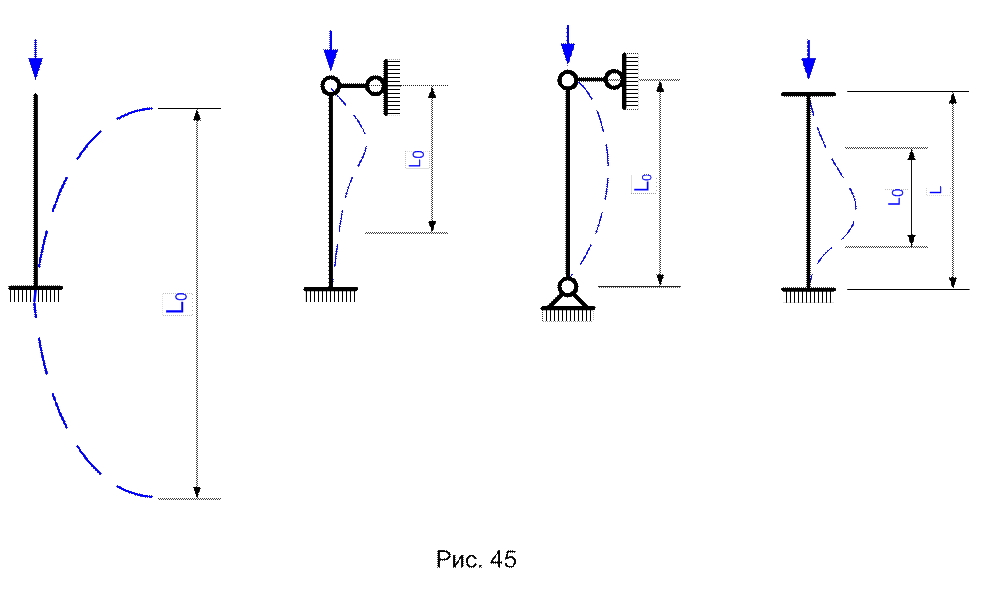
            Эти данные полезно и понимать и запомнить, т.к. зная l и характер закреплений, мы легко уточняем расчетную длину стержня

l₀ = μl                                               (39)

            и наоборот, зная μ мы должны ясно представлять характер концевых закреплений стержня, идею их конструкции (конструктивного решения). Отношение расчетной длины стержня к радиусу инерции его сечения ( имеется в виду постоянное по длине) определит гибкость стержня

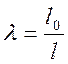                                                    (40)

            Если сечение имеет главные оси и (или) стержень закреплен в двух направлениях по разному, то мы приходим к необходимости определения и λ_х иλ_у. В случае λ_х ≠ λ_у – стержень неравногибок, неравноустойчив; в случае λ_х = λ_у – стержень равноустойчив. Подчеркнем – чем стержень более равноустойчив, тем он лучше запроектирован. Для оценки влияния гибкости на несущую способность стержня используем известное выражение для критической силы по Эйлеру

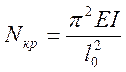,                                                   (41)

            где EI – изгибная жесткость стержня. Переходя от N_кр к критическим напряжениям, т.е. разделив обе части (41) на площадь сечения, получим

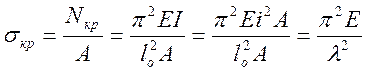                              (42)

            Здесь для преобразований использованы известные из курса сопротивления материалов выражение для определения радиуса инерции

,

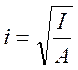            откуда I = i²A, и выражение (40) для определения гибкости. Заметим, что конечная запись σ_кр по (42) справедлива только для гибких стержней, когда λ > 0. Уровень критических напряжений будет снижаться при наличии каких-либо эксцентриситетов, поэтому считается, что общая устойчивость центрально-сжатого стержня будет обеспечена при

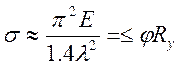,                                          (43)

            где коэффициент 1,4 учитывает наличие случайных эксцентриситетов; φ –коэффициент продольного изгиба. Отсюда в предельном состоянии (вместо «меньше-равно» используем «равно») имеем

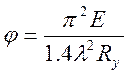,                                       (44)

            Зависимость φ от λ и R_y в форме (44) можно представить графически, например на рис. 46.

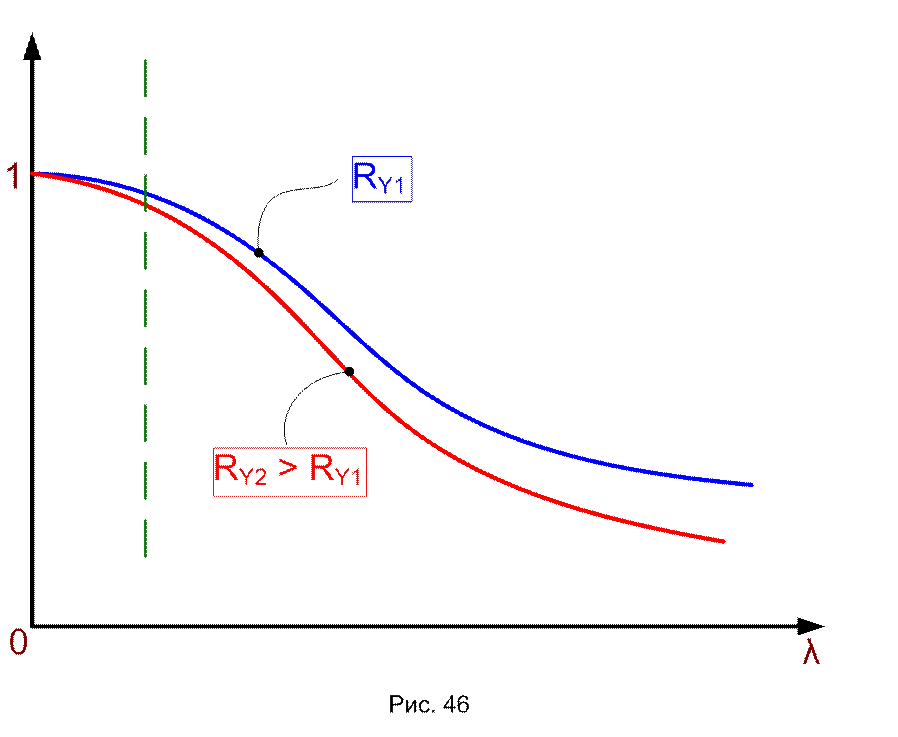
            Анализируя (44) и графики рис. 46, можно заметить, что при λ → 0 (гибкость стержня снижается) φ – увеличивается; при λ =0 (негибкий, т.е. абсолютно жесткий стержень) φ = 1; при увеличении гибкости (его способность воспринимать сжатие снижается) φ – уменьшается; при λ = ∞ (абсолютно гибкий, не жесткий стержень) φ =0 – или, в иной записи, при 0 ≤ λ ≤ ∞ имеем 1≥ φ ≥ 0 с совершенно конкретным физическим смыслом – φ =0 – стержень не способен воспринимать сжатие, т.к. очень гибок; φ =1 – стержень не способен терять устойчивость, он работает на сжатие без продольного изгиба, т.к. очень жесток. Также из (44) достаточно очевидно, что увеличение прочности стали (при постоянной гибкости) снижает коэффициент продольного изгиба и практически не увеличивает произведение φR_y  в  (43), поэтому общепризнанно, что применение высокопрочных сталей в центрально-сжатых элемента, как правило, экономически неоправданно.

            На рис.46 зона λ ≈ 0 отделенная пунктирной линией – условно. Поэтому СНиП [1, п. 5.3] дает иные формулы для вычисления коэффициента изгиба. Но на практике обычно ни (43), ни формулы [1, п. 5.3] не используется, а коэффициенты φ определяются по [1, табл. 72] в функции λ и R_y с линейной интерполяцией, при необходимости. При этом проверка общей устойчивости центрально-сжатого стержня выполняется по формуле

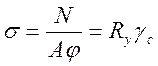,                                        (45)

            где, как и раньше, γ_с – коэффициент условия работы элемента, уточняемый по [1, табл. 6]. Если (45) переписать в форме

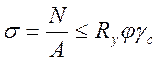                                        (46)