Конструкционная характеристика стали. Основы расчета стальных конструкций. Соединения стальных конструкций. Проектирование конструкций балочной клетки. Проектирование центрально сжатых стержней, страница 12

R_б.н. = Q_max  = (q_noγ_fq + p_noγ_fp)А′_гр, где

         А′_гр = 0,5 А_гр.б.н. – заштрихована на рис.17,а вертикально. Во втором варианте, когда n ≥ 5, схему нагрузки можно упростить более полно, рассматривая общую грузовую площадь для второстепенной балки как сумму частных – тогда фактическая нагрузка по рис. 17.е примет условный (эквивалентный) вид по рис.17,ж, где qn и q определяются по формулам (18, 19).

         Пример 4. На рис.18,а приведен фрагмент усложненной компоновки клетки при комбинированном сопряжении (напомним – балки настила опираются этажно на второстепенные, которые понижено примыкают к главным). Уточнение расчетной схемы балки настила через грузовую площадь (заштрихована с наклоном вправо) в данном случае совершенно аналогично рассмотренному в примере 1. Схема фактической нагрузки по рис. 18,б, где qn и q определяются по формулам (18, 19), - проста и отвечает характеру грузовой площади.

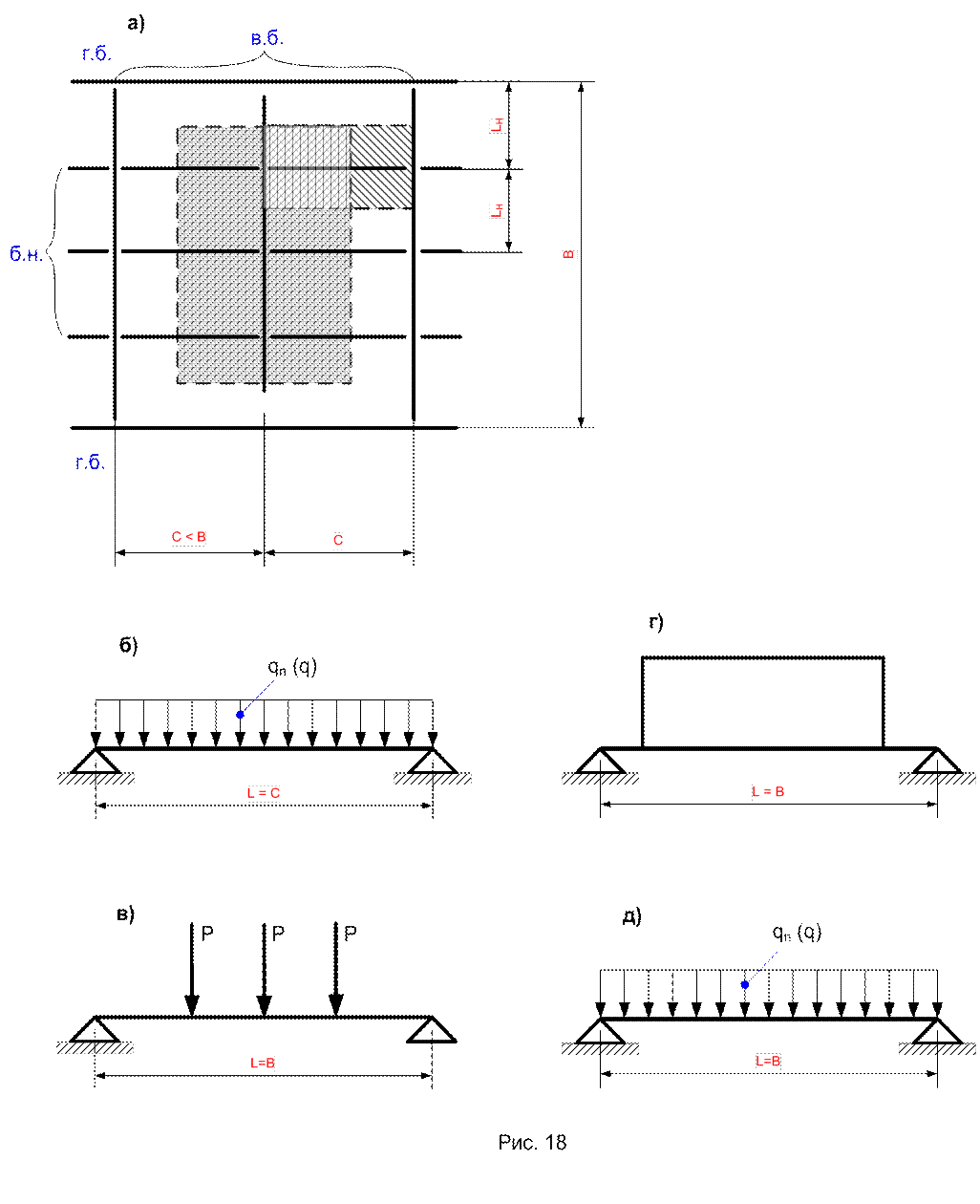
         Второстепенная балка, средняя, воспринимает нагрузку только от опирающихся на нее балок настила в виде сосредоточенных сил Р = 2R_б.н.. R_б.н. определяется как в примере 3, причем А′_гр заштрихована на рис.18,а вертикально. При этом количестве (n < 5) фактическая схема нагрузки, рис.18,в, используется без изменений. При их большом количестве (n ≥ 5) схему фактической нагрузки можно представить в виде рис.18,в (грузовая площадь на рис.18,а заштрихована с наклоном влево), перейдя затем с небольшой погрешностью к условной равномерно распределенной, по рис.18,д, где qn и q определяются по формулам (18, 19).

         Статический расчет балки выполняется обычным образом, всегда и только от расчетных нагрузок, с построением эпюр М и Q и дополнительным определением максимальных изгибающего момента М_max и поперечной силы Q_max (опорной реакции).

Определение требуемых геометрических

характеристик сечения балки.

         К ним относятся минимальные (обычно этот термин заменяется иным – требуемые) момент сопротивления W_тр и момент инерции I_тр.

         Для определения W_тр используем запись условия обеспечения прочности балки, как изгибаемого элемента в форме (2) (см. табл. 1)

σ =  ≤ R_yγ_cC                                 (20)

         Анализируя ее, видим, что кроме W все компоненты известны: М=М_max; R_y, γ_c – принимаются по [1, табл. 51 и 6, соответственно]; с = 1.12 – для балочного проката [1, табл. 66], а в общем случае по [1, п. 5.18 и др.], - поэтому

W_тр  ≥

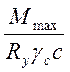
         Для определения I_тр используем условия обеспечения жесткости балки в форме (5) (см. табл. 2) при равномерно распределенной нагрузке:

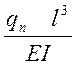= ≤                                 (22)

         при нагрузке, отличающейся от равномерно распределенной, и отсутствии (или сложности получения) точной формулы относительного прогиба

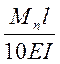 ≈  ≤                                  (23)

         Анализируя их, видим, что кроме I все компоненты известны: q_n, 1 – из расчетной схемы; М_n = M_max(q_no + p_no)/(q_noγ_fg + p_noγ_fp); Е = 2.1х10^{6 кг}/_см² – модуль упругости прокатной стали [1, табл.63]; n = 250 – [1, табл.40], - поэтому

I_mp ≥ 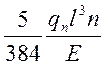                                       (24)

         или

I_mp ≥ 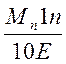                                 (25)

         Подбор сечения по сортаменту производится простым выбором возможных профилей, фактические геометрические характеристики сечений которых W_ф, I_ф не меньше требуемых, т.е. удовлетворяют условиям W_ф ≥ W_тр, I_ф ≥ I_тр. Для балок настила швеллеры и двутавры равноприменимы, поэтому предпочтение следует отдавать более легким сечениям, а при равенстве погонных масс – имеющим большие геометрические характеристики. Так как балки настила подходят к второстепенным с двух сторон, последние удобнее иметь двутавровыми, что и является определяющим при подборе их сечений.

         4.5. Подбор сечений составных балок.