Конструкционная характеристика стали. Основы расчета стальных конструкций. Соединения стальных конструкций. Проектирование конструкций балочной клетки. Проектирование центрально сжатых стержней, страница 14

Определение требуемых геометрических

характеристик сечения балки

         - W_тр, I_тр, в принципе сходно с тем, что используется при подборе прокатных сечений. Но главные балки являются весьма ответственными, нередко имеют переменное сечение и чаще, по признакам [1, п. 5.18], проектируются в упругой стадии работы стали, без учета развития пластических деформаций, т.е. при коэффициентах пластичности с = 1. Поэтому в отличие от (21) здесь требуемый момент сопротивления сечения

W_тр ≥ 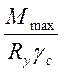                                 (26)

         Для определения требуемого момента инерции в зависимости от характера нагрузки применимы  выражения (24) и (25), но по нормам [ 1, табл. 40] – n = 400.

         Подбор сечения составной балки. В общем случае сечение балки можно составить, скомпоновать из разных прокатных элементов. Некоторые примеры таких сечений показаны на рис.24.

         Примерно до середины 60-х гг. это были сварные и клепаные балки, впоследствии и сегодня – практически только сварные. Наиболее распространенным является сечение, составленное из листовых элементов (прочие следует рассматривать как частные решения, используемые в увязке с наличным материалом). Его компоновку рассмотрим более подробно.

         На рис.25 приведены основные параметры (размеры) листового сечения с символикой, отвечающей [1]: W – символ стенки балки, f – символ пояса (поясов или полок) балки.

                                 

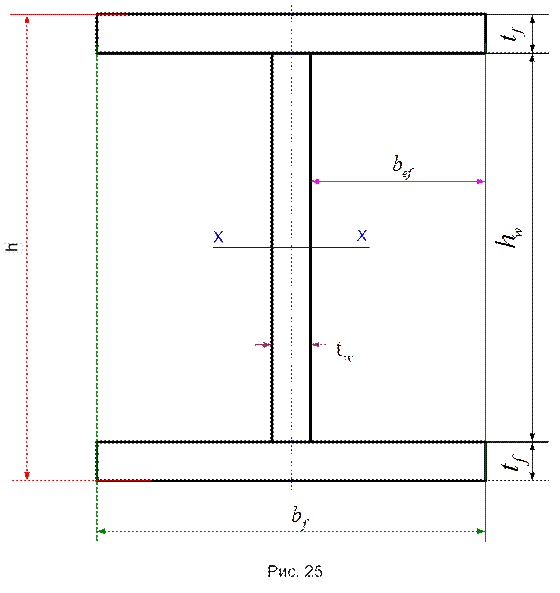
         Все они – h, t_w, t_f, b_f – подлежат определению (назначению) в результате

 компоновки. Но предварительно полезно представить себе некоторые связующие их соотношения, отчасти сложившиеся статически, отчасти подсказанные нормами [1] с учетом разносторонних аспектов обеспечения нормальной работы балки:

         h ≈ (1/8…1/12)l; b_f ≈ (1/3…1/5)h; λ_w ≈ h_w/t_w ≈ 80…140 – гибкость стенки, λ_f =  

гибкость свеса пояса и ее предельное значение, гарантирующее обеспечение его местной устойчивости при продольном сжатии (например, верхний пояс балки) [1, п. 7.24], b_ef – свес пояса, поясного листа, полки, рис.25; более узко – 5 мм ≤ t_w < t_f; t_w < t_f ≤ 40мм; 200мм ≤ b_f ≤ 400мм.

         Получив представление об основных пропорциях элементов сечения балки, можно приступать к его компоновке. Для этого удобно использовать расчетный алгоритм, поддающийся к тому же и программированию для использования ЭВМ.

         1. Ориентировочно назначаем высоту балки в пропорции от пролета, например,

h′ = 1/10.

      2. Уточняем толщину стенки балки – t_w. Из условия среднестатистической гибкости λ_w ≈ 120, часто достаточной для обеспечения в дальнейшем ее местной устойчивости, найдем

t_wcт  ≈ h′/120                                (26)

         Из условия обеспечения местной прочности стенки при действии максимальных касательных напряжений

τ_{max ≈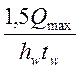}  ≤ R_sγ_c, где

         R_s = 0,58 R_y [1, табл.1], при h_w ≈ h′, найдем

t_wmin ≥ .

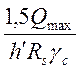         Если t_wcт > t_wmin, то t_w  = t_wcт с округлением до целых «мм» в меньшую сторону. Если t_wcт < t_wmin, то t_w  = t_wmin с округлением до целых «мм» в большую сторону. В общем можно сказать, что из (26) и (27) следует принимать большее значение, разумно округляя его до целых «мм» (иногда еще и до четных).

         3. Уточняем высоту балки, понимая, что в п.1 она была принята без какого-либо обоснования. Не вдаваясь в детальный анализ, можно определить площадь сечения стенки балки как

A_w = h_w х t_w ≈  ≈ a₁ ≈ a₁h²,

         т.е. в форме, отвечающей параболической зависимости. На графике А = f(h), рис.26, ее представим кривой А_w.

      

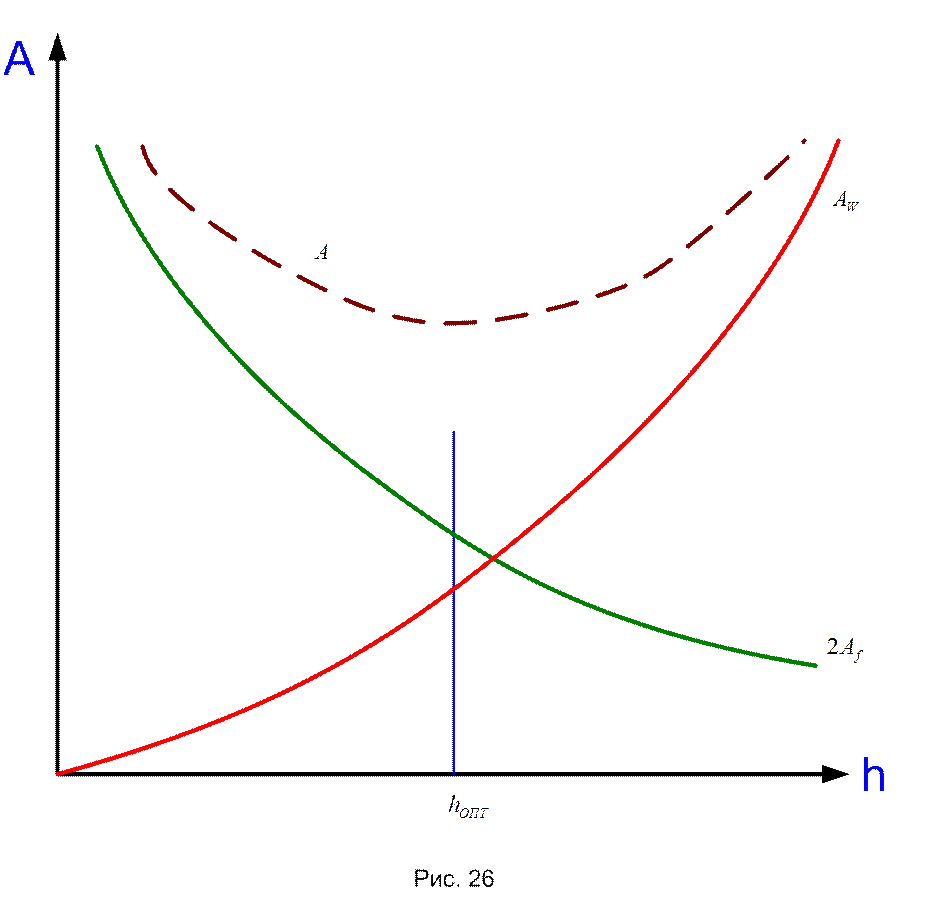
         Также просто можно найти зависимость суммарной площади поясов балки от ее высоты, например, в форме

2A_f ≈  ≈ ,

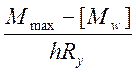         Представляющий гиперболу, см. рис.26; а₁, а₂ – некоторые постоянные. Складывая их, найдем характер зависимости площади сечения балки (пунктир на графике) от высоты балки. Она имеет очевидный минимум при h_опт, отвечающий условию 2А_f/A_w ≥ 1 и называется «оптимальной». Эта высота определяется по формуле: