Конструкционная характеристика стали. Основы расчета стальных конструкций. Соединения стальных конструкций. Проектирование конструкций балочной клетки. Проектирование центрально сжатых стержней, страница 11

         Пример 1. На рис.15,а показан фрагмент нормальной компоновки клетки при этажном сопряжении.

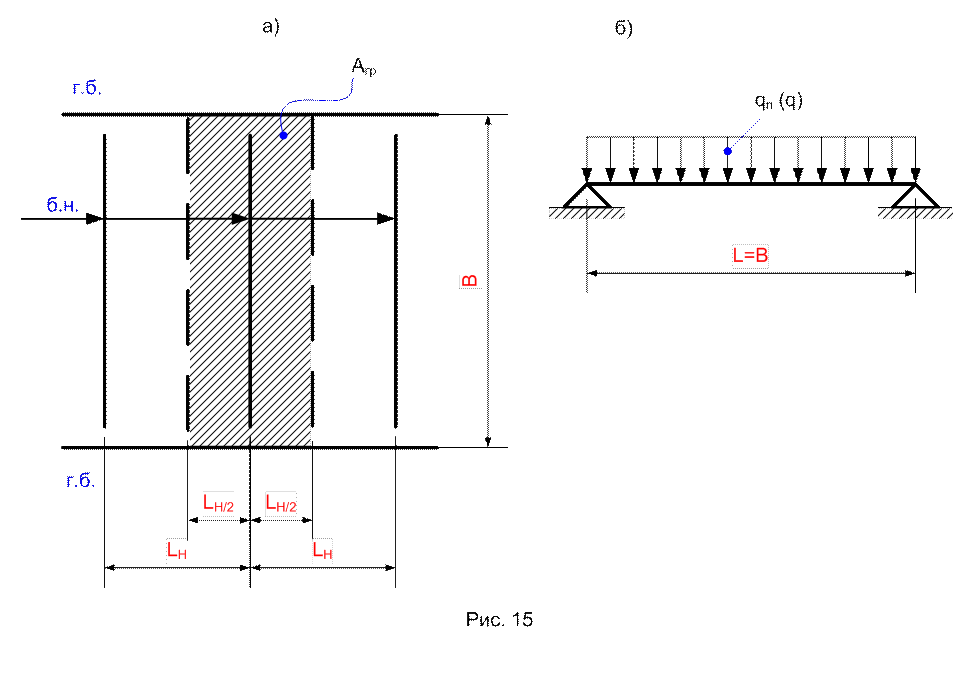
         Настил подкреплен, опирается только на балки настила, поэтому, введя разграничительные срединные линии (пунктиры между соседними балками), найдем форму грузовой площади для средней балки – выделена штриховкой. Ее площадь А_гр=Вl_н – прямоугольная, следовательно нагрузка на балку будет равномерна по всему пролету, а расчетная схема будет иметь вид по рис.15,б, где

q_n = ( q_no + p_no ) ,                            (18)

q = (q_noγ_{fg +}  p_noγ_fp)                        (19)

         - соответственно нормативная и расчетная погонные нагрузки.

         Записи вида (18,19) – справедливы для любой формы грузовой площади, но в частном случае, когда она прямоугольна, могут быть приведены к виду

q_n = ( q_no + p_no)l_н;  q = (q_noγ_fg + p_noγ_fp)l_н, т.е.

         q_n  и q зависит и может определятся не по величине А_гр, а по ширине грузовой площади – в данном случае l_н.

         Пример 2. На рис.16,а показан фрагмент нормальной компоновки клетки при сопряжении в уровне.

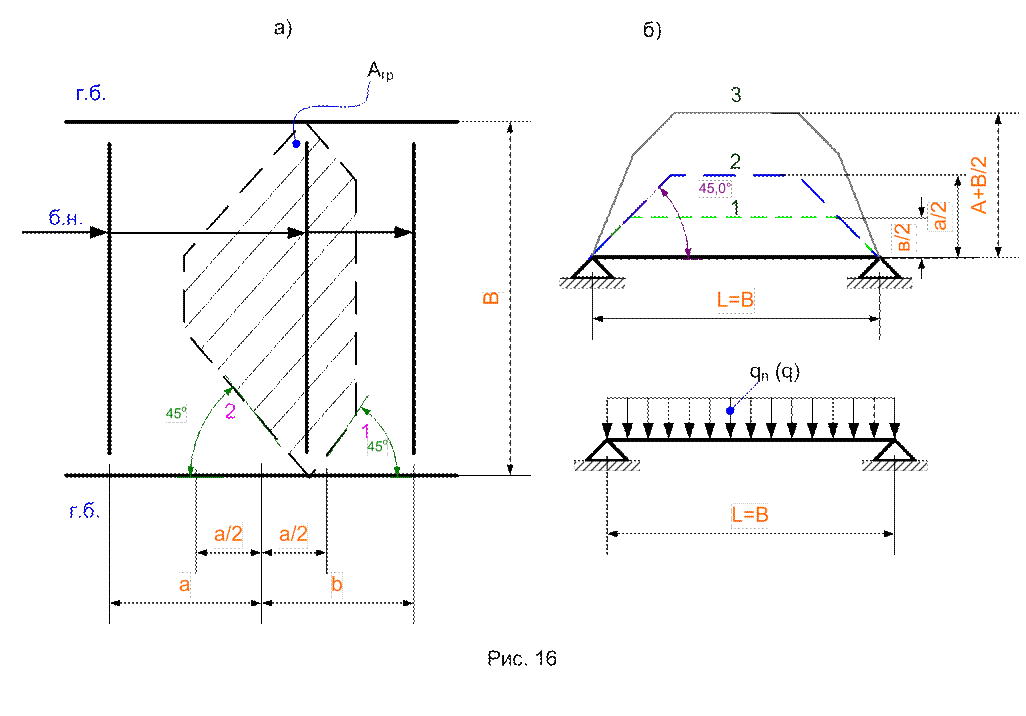
         Настил опирается и на балки настила и на главные балки, поэтому фориа грузовой площади здесь (заштрихована) не получается прямоугольной. Так как разграничительные линии между сходящимися под углом балками являются биссектрисами этих углов, то можно сказать, что выделение грузовых площадей выполняется с применением «правила биссектрис» (напомним – правило биссектрис используется только и всегда при сопряжении балок в уровне). Если по разграничительным срединным линиям произвести разрез и согнуть правую 1 и левую 2 части фигуры А_гр по оси средней балки, то увидим, рис.16,б – пунктиры, что балка по длине загружена равномерно. Фактически характер нагрузки, показанный линией 3 (получена сложением ординат 1 и 2) – достаточно сложен и, главное, не удобен для последующего подсчета, поэтому на практике его обычно упрощают. Достигается это переходом к равномерной, эквивалентной нагрузке – рис.16,в, определяемой по формулам (18, 19). Такой переход от сложной фактической нагрузки, к условной (эквивалентной), но по характеру простой, содержит некоторую погрешность, однако для целей инженерного расчета она, как правило и как можно убедиться, вполне допустимая (≤10%).

         Пример 3. На рис.17,а приведен фрагмент усложненной компоновки клетки при сопряжении всех балок в уровне.

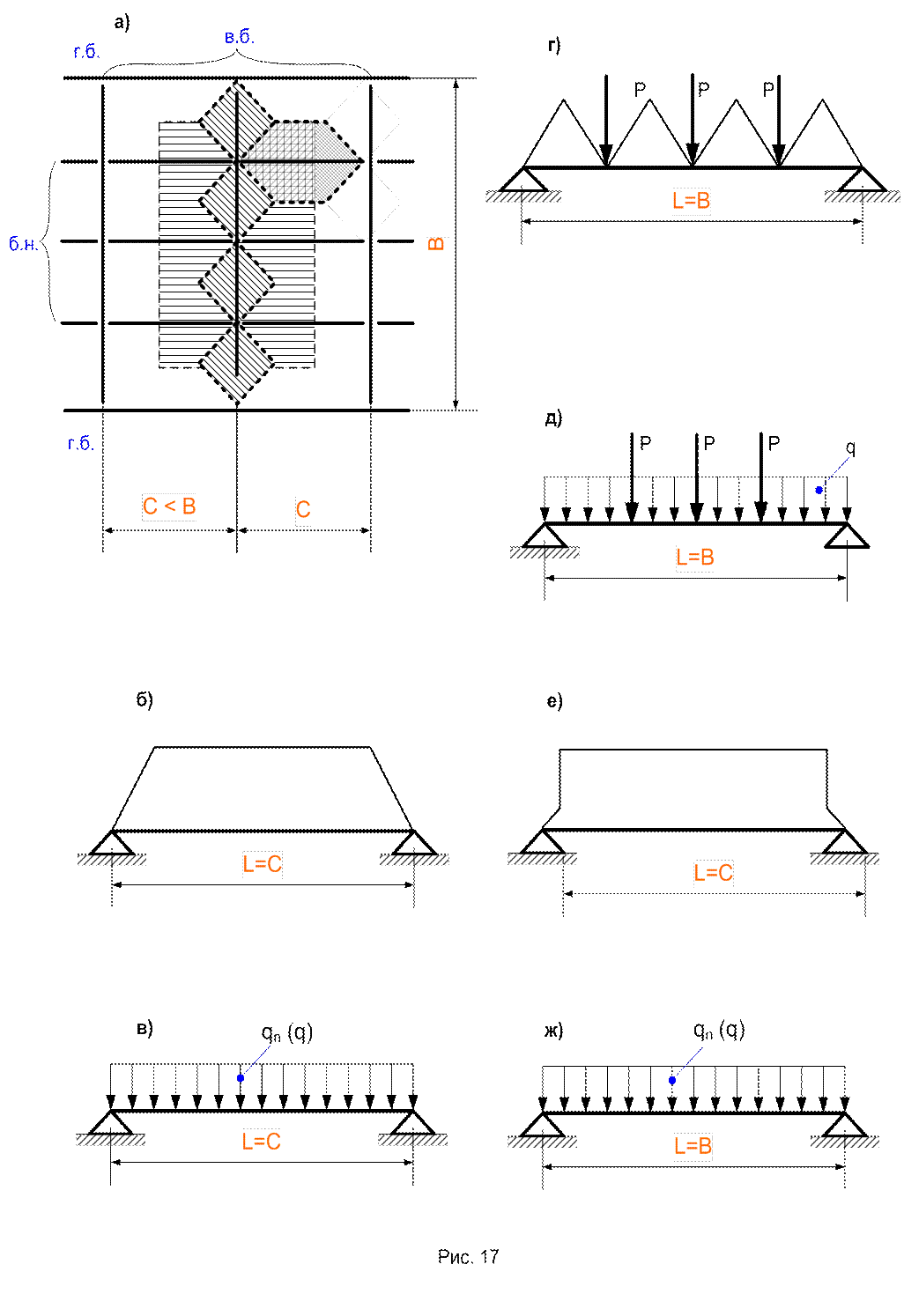
Уточнение расчетных схем балок настила и вспомогательных балок может быть выполнено как последовательно, так и независимо (например, при реконструкции и решении каких - либо  проблем, касающихся только второстепенных балок). Так как настил на все балки, то разграничительные срединные линии проводятся как и в предыдущем примере, т.е. с использованием правила биссектрис. Грузовая площадь для рядовой балки настила заштрихована с наклоном вправо. В соответствии с ней фактическая нагрузка имеет вид по рис. 17,б, а условная (эквивалентная) – по рис.17,в, где q_n и q определяются по формулам (18, 19).

         Уточняя расчетную схему второстепенной балки видим, что она воспринимает нагрузку как непосредственно от настила – грузовая площадь заштрихована на рис.17,а с наклоном влево, так и от примыкающих к ней с двух сторон балок настила, поэтому в общем случае фактическая нагрузка имеет вид по рис.17,г. От этого общего случая можно перейти к двум частным вариантам: первый – когда количество сосредоточенных сил Р = 2R_б.н. меньше пяти (n < 5), второй – когда их количество пять и более (n ≥ 5). В первом варианте можно упростить только схему распределенной нагрузки, перейдя к условной (эквивалентной) равномерно распределенной по формуле (19), определяя только ее расчетное значение, и получив расчетную схему по рис.17,д.

         Следует иметь ввиду, что R_б.н. – опорная реакция (Q_max) балки настила может быть при последовательном решении взята из статического расчета балки настила, при независимом решении (когда балки настила не рассматривались) найдена по формуле