Физика \ Физика

Учебное пособие по физике. Часть II. Молекулярно-кинетическая теория, страница 8

Пусть в некотором сосуде заключен газ. Молекулы, двигаясь хаотично, сталкиваются со стенками сосуда и производят давление. Это явление определяется числом ударов, производимых молекулами за единицу времени на единицу площади поверхности сосуда.

Сила ударов молекулы, а, следовательно, и давление молекулы зависит от скорости и массы молекул. Но от скорости и массы молекул зависит кинетическая энергия, следовательно, имеется возможность выразить давление газа на стенки сосуда через кинетическую энергию молекул и их число.

Вычисления показывают, что давление газа будет

P=(2/3)nWk

где n - число молекул в единице объема. Это уравнение называют основным уравнением кинетической теории газов. Таким образом, среднюю кинетическую энергию молекул газа можно найти:

Wk=(m0ν2KB)/2, Wk=kT3/2, Wk=(3p)/(2n)

Внутренняя энергия идеального газа

Внутренняя энергия идеального одноатомного газа легко вычисляется. Вспомним, что молекулы идеального газа не взаимодействуют из-за наличия больших межмолекулярных промежутков и, как условились ранее, энергия взаимодействия равна нулю. Значит, внутренняя энергия идеального газа определяется только кинетической энергией движения молекул

U=ΣWk=NWk

где N - число всех молекул газа, а Wk – средняя кинетическая энергия одной молекулы. Вычислим внутреннюю энергию идеального газа, учитывая, что где m  - масса всего газа, νкв – средняя скорость молекул. Теперь учтём, что

Wk =kТЗ/2,

тогда U=N(3/2)kT=(3/2)(m/M)NAkT, где m/М - число киломолей,

NA – число Авогадро Произведение NA k заменим одной постоянной величиной R, которую называют универсальной газовой постоянной, т.е. R=NAk. Учитывая это обозначение

U=(3m/2M)RT,

Причём  R=6,023×1026 1/кмоль×1,38-23Дж/К=8,314×103Дж/кмольК

Существует ещё один путь вычисления внутренней энергии, через основное уравнение кинетической энергии

U=3p/2n=(3/2)p(n/N)=(3/2)pN

Таким образом, мы проследили возможные пути вычисления внутренней энергии идеального газа.


Уравнение Клапейрона – Менделеева

Состояние любого газа характеризуется его массой,давлением, объемом итемпературой.При изменении одного из параметров изменяются и другие параметры, значит, между ними существует определенная связь, которую легко установить. Вспомним,  что внутреннюю энергию газа можно находить

U=(3/2)pV и  ν=(3/2)(m/M)RT.

Так как речь идет о внутренней энергии одного и того же газа, то рV/2 = 3RTm/2M =>pV=RTm/M, полученное уравнение называют уравнением Клапейрона - Менделеева. Произведение давления и объема газа равняется произведению числа киломолей, универсальной газовой постоянной   и абсолютной температуры.

Нетрудно заметить, что уравнение Клапейрона - Менделеева отражает закон сохранения энергии для идеального газа.

Частные случаи уравнения Клапейрона - Менделеева

Если в уравнении Клапейрона - Менделеева принимать некоторые из параметров постоянными, то получим ряд частных уравнений:

1 m=CONST,  pV=RTm/M=>pV/T=CONST

Это уравнение часто называют уравнением состояния идеального газа или объединенным газовым законом. Его часто записывают в следующей форме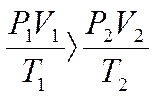   

2 Допустим, что m=CONST и T=CONST

Такие процессы называют изотермическими. Учитывая это, нетрудно заметить, что в уравнении pV=RTm/M, правая часть будет постоянной при любых изменениях давления и объема pV=CONST или же p1V1= p2V2 .При постоянной массе и температуре объём газа обратно пропорционален давлению закон Бойля-Мариотта.

В координатах p, V процесс изображается гиперболой. Рисунок 10

3 m=CONST и V= CONST. Процесс с постоянным объемом называют изохорическим.

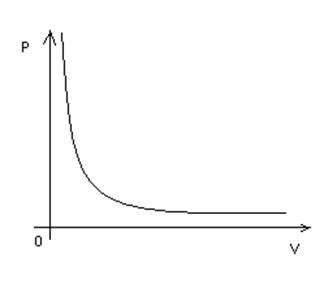
Рисунок 10 – изотермический процесс

Используя уравнение Клапейрона – Менделеева, установим, что:

pV=RTm/M => p/T×m/M×RV, то есть p/T=CONST

Или же р1/Т1=р2Т2 . При изохорическом процессе давление идеального газа прямо пропорционально его абсолютной температуре. Эта связь была открыта французским физиком Шарлем и называется закон Шарля. График процесса изображен на рисунке 11.

Скачать файл