Учебное пособие по физике. Часть II. Молекулярно-кинетическая теория, страница 6

где Q - количество теплоты. Если теплообмен идет между несколькими телами, то Σ_отдQ=ΣQ_получ, то есть наблюдается, так называемый, тепловой баланс. Когда внутренняя энергия тела изменяется, то тело нагревается или охлаждается; плавится или затвердевает; испаряется или конденсирует, сгорает. Многочисленные опыты подтверждают, что в тепловых процессах, как и в любых других, имеет место закон сохранения и превращении энергии, то есть, энергия не возникает и не исчезает, а только передается от одного тела к другому или превращается из одного вида в другой, количественно сохраняясь. При наличии работы и теплообмена этот закон можно написать:                                        ΔU=A+Q

Закон сохранения энергии применительный к тепловым процессам называют первым началом термодинамики.

Идеальный газ

Любое вещество может находиться в твердом, жидком и газообразном состоянии. Для газа характерны большие промежутки между молекулами r>r₀, а силы молекулярного взаимодействия пренебрежимо малы. Молекулы обладают большими скоростями  поступательного движения. Для простоты не будем учитывать размеры молекул газа, представим газ как множество материальных точек, между которыми отсутствуют силы молекулярного взаимодействия. Двигаясь хаотически, молекулы сталкиваются друг с другом, как упругие шарики. Такой газ называют идеальным. Движение молекул между последующими столкновениями можно считать равномерным и прямолинейным. Внутренняя энергия такого газа будет определяться только кинетической энергией его молекул.

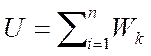
Энергия взаимодействия молекул идеального газа принимается за ноль, т.к. r>r₀. Для определенной молекулы кинетическая энергия находится по формуле:

W_k=m₀ν²/2

где ν - скорость движения молекулы

Скорости газовых молекул.

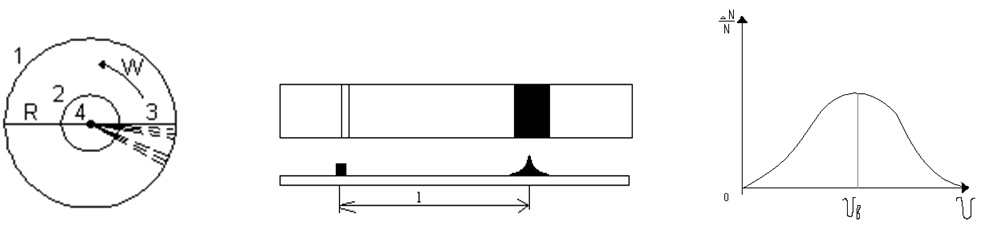
Опыт Штерна

Для определения кинетической энергии молекул необходимо знать массу молекулы и её скорость

W_k=m₀ν²/2

Массу молекулы можно найти косвенным путем

m₀=M/N_A

Рисунок 4 – опыт штерна

Определение скоростей молекул связано с определенными трудностями. Впервые скорость молекул определил опытным путем немецкий физик Штерн в 1920 году. Идею опыта можно понять из рисунка. Два жестко связанных цилиндра 1 и 2 герметично закрыты и из них тщательно откачен воздух. В стенке малого цилиндра 1 сделана щель, формирующая узкий пучок молекул серебра, который испаряется с поверхности нити 4 электрическим током. Молекулы оседали на холодной стенке большого цилиндра, образуя четкую полоску. При вращении цилиндров пучок смещался и несколько рассеивался. Вновь образованная полоска получается несколько размытой и имеет форму холма. Скорость молекул можно найти из следующих соображений. Время пролета молекул определяется из уравнения движения: χ = νt: т.к. χ = R, то t=R/χ. За это же время смещение молекул будет

l=ωRt

Отсюда находим, что R/ν=l/ωR и ν=ωR²/l.

Опыт Штерна позволяет сделать следующие выводы:

1 Скорости молекул при одной и той же температуре различны (размытость полоски);

2 Скорости молекул с увеличением температуры возрастают (растет смещение 1);

3 Скорости молекул зависят от их массы и с увеличением массы молекул скорости уменьшаются. Если по оси абсцисс отложить значение скорости, а по оси ординат  относительное число молекул, скорость которых лежит в интервале от ν до ν+Δν, т.е. число ΔN/N, то получим кривую распределения молекул по скоростям. Скорость, соответствующая максимуму кривой, называют наиболее вероятной. Кроме наиболее вероятной скорости в физике используется средняя скорость

ν=(ν₁+ν₂+...+ν_n)/n

и средняя квадратичная скорость

ν_кв=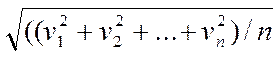

Все эти скорости несколько отличаются, но могут быть, выражены одна через другую. Определив на опыте, например, наиболее вероятную скорость, можно вычислить среднюю и среднюю квадратичную скорости. Следует заметить, что кривую распределения скоростей молекул задолго до опыта теоретически рассчитал английский физик Максвелл. В дальнейшем будем обращаться в основном к средней квадратичной скорости. Величина ее для некоторых веществ при различной температуре приведена в таблице: