Учебное пособие по физике. Часть II. Молекулярно-кинетическая теория, страница 7

Таблица № 1– Скорости молекул в м/с при температурах.

Вещество	Масса молекул (кг)	0º	100º	200º	300º
H2O	3*10-26	615	700	810	890
O2	5.33*10-26	460	520	605	665
Ag	18*10-26	250	285	330	360

Абсолютная температура как мера средней кинетической энергии молекул.

Абсолютный ноль.

Абсолютная шкала температур и шкала Цельсия

Как указывалось выше, средняя кинетическая энергия  поступательного движения молекул находится:

W_k=m₀ν_кв²/2

Вычислим эту энергию для некоторых веществ при различных температурах и результаты занесём в таблицу. (Энергия измеряется в Джоулях).

Таблица №2

Вещество	Масса молекул (кг)	0º	100º	200º	300º
H2O	3*10-26	5,66*10-21	7,4*10-21	9,8*10-21	11,88*10-21
O2	5,33*10-26	5,6*10-21	7,2*10-21	9,8*10-21	11,8*10-21
Ag	18*10-26	5,6*10-21	7,3*10-21	9,8*10-21	11,8*10-21

Анализируя зависимость W_k=f(tº) можно заметить, что при одной и той же температуре средняя кинетическая энергия движения молекул любого тела остается одной и той же. Это исключительно важный вывод. Средняя кинетическая энергия движения молекул определяется температурой тела. Из таблицы видно, что с ростом температуры средняя кинетическая энергия увеличивается

W_k=tº+W₀

Где W₀=5,66×10^-21 Дж

Чтобы найти коэффициент, нужно b=ΔW_k/Δtº.

Вычисление показывает, что b=2,07×10^-23 Дж/град, а уравнение запишется W_k=2,07×10^-23 tº+5,66×10^-21 Таким образом, мы получим уравнение, выражающее зависимость средней кинетической энергии от температуры. Найдем температуру, при которой W_k=0. Допустим, что линейная зависимость сохраняется и при низких отрицательных температурах. Сделав такое предположение, находим

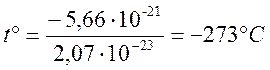
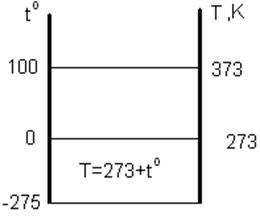
 Более точные вычисления показывают, что эта температура будет  -273,15°С. При такой температуре среднюю кинетическую энергию движения молекул можно считать равной нулю. Значит, при данной температуре прекращается движение молекул идеального газа. Нетрудно сделать вывод, что ниже указанной точки понятие температуры теряет свой смысл. Эта предельно  низкая температура в природе. Она называется абсолютным нулем. Английский физик Кельвин предложил -273 °С принять за 0, сохраняя при этом температурные интервалы. Тогда по шкале Кельвина не будет отрицательных температур, и ее назвали абсолютной шкалой. Связь температуры по шкале Кельвина и шкале Цельсия легко установить из указанного рисунка. Т = t°+273, где Т- температура по шкале Кельвина. Если теперь построить график   зависимости средней кинетической энергии от абсолютной температуры, то он несколько изменится.

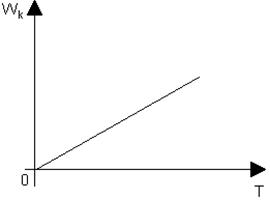
Это изменение заключается в том, что он начинается из нуля, а линейная формула графика сохранится. Такую зависимость записывают так W_k=b×T и называют прямой пропорциональной, где, как указывалось, b=2,07×10^-23 Дж/К. Немецкий физик Больцман предложил это уравнение записывать в следующей форме: W_k=(KT)×3/2 , где коэффициент К=b×2/3 и, проделав вычисления, находим, что К=1,38×10^-23 Дж/К. Этот коэффициент называется постоянной Больцмана. Таким образом, средняя кинетическая энергия движения молекул прямо пропорциональна абсолютной температуре и не зависит от природы газа. Поведение вещества при температуре, близкой к абсолютному нулю представляет огромный интерес для современной физики. Многие вещества при сверхнизких температурах проявляют совершенно неожиданные свойства, такие как сверхпроводимость, сверхтекучесть. Надо заметить, что при абсолютном нуле движение молекул не прекращается – они совершают так называемые колебания, да и сама линейная зависимость вблизи абсолютного нуля нарушается.

Основное уравнение кинетической теории газов