Учебное пособие по физике. Часть II. Молекулярно-кинетическая теория, страница 30

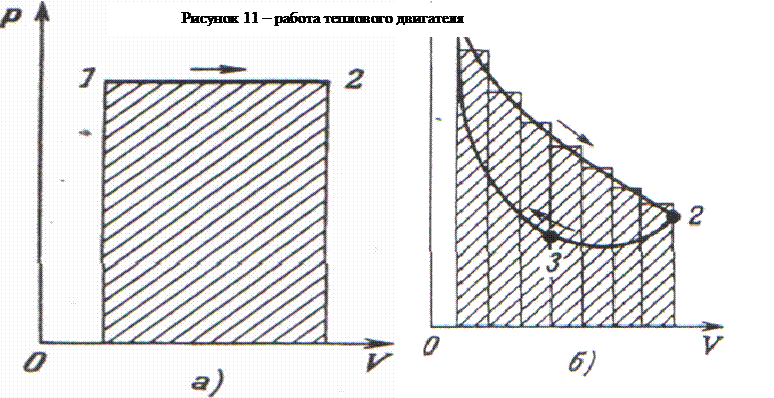
Если же давление при расширении газа все же меняется, то такой процесс можно представить в виде последовательного ряда микропроцессов, в ходе которых небольшие изменения объема ΔV_i происходят при хотя и разных, но постоянных значениях p_i. Сказанное можно проиллюстрировать графиками зависимости p(V), представленными на рисунке 11(а, б). Работу А, совершаемую газом при расширении в первом случае, можно рассчитать как площадь прямоугольника, во втором - найти как сумму прямоугольников, на которые разбита площадь под кривой 1-2. При сжатии газа (переходе из точки 2 в точку 1 на рисунке 11,б) приходится совершать работу А. Но |А|=|A'| только в случае, если мы попытаемся осуществлять сжатие, следуя кривой 2-1. Если же мы сжимаем газ, следуя, например, кривой 2-3-1, то затратим меньшую работу |A|>|A'| (площадь под кривой 2-3-1 меньше, чем под кривой 1-2). Но в итоге мы вновь вернем газ в состояние 1, то есть завершим цикл, в результате которого будет произведена работа ΔA = А -А'.

Вспомним теперь первое начало термодинамики - ведь сама по себе работа ΔA ниоткуда не возьмется. В нее должна превратиться часть тепла, которое мы сообщаем газу. При этом из всего тепла Q₁, сообщенного газу на участке 1-2, часть его Q₂ должна быть отдана окружающей среде на участке 2-3-1 при сжатии газа. В итоге ΔA=Q₁-Q₂. Отметим также, что в результате совершения цикла 1-2-3-1 внутренняя энергия газа не изменится, поскольку начальная температура будет равна его конечной температуре (точно так же примут свои начальные значения p и Q). Подобные циклы, в которых рабочее тело (газ) периодически совершает работу основа действия большого числа тепловых машин. В таких машинах источник теплоты Q₁ называется нагревателем, а охлаждающий элемент конструкции, забирающий теплоту Q₂  - холодильником. Очевидно, что чем больше производимая такой машиной работа ΔA  (при том же потребляемом количестве теплоты  Q₁), тем больше эффективность такой машины.

Отношение ΔA / Q₁  носит название коэффициента полезного действия (КПД):

η= ΔA / Q₁  =( Q₁-Q₂)/Q₁=1-Q₂/Q₁

Часто КПД измеряют в процентах:

η =( Q₁-Q₂)/Q₁×100%

Из закона сохранения энергии следует, что нельзя получить КПД больше единицы, то есть невозможно построить такой двигатель, который производил бы работу большую, чем затраченная на это энергия. Но вот о том, как построить машину с максимально возможным КПД, задумывались многие изобретатели. На заре развития техники предлагалось много решений, в том числе - совсем экзотических, например, использовать в машине, а качестве рабочего тела (газа) пары молока, вина и т.д. Лишь в начале прошлого века французский инженер С.Карно доказал, что максимально возможный КПД тепловой машины не зависит от природы рабочего тела, а определяется лишь температурой нагревателя Т₁ и холодильника Т₂ :

η =( Т₁-Т₂)/Т₁=1-Т₂/Т₁

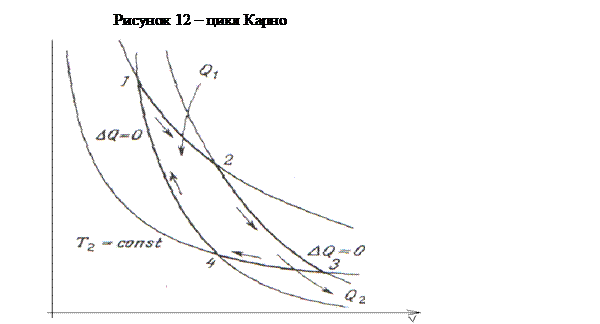
Но такой КПД способна иметь лишь идеальная машина; у реальных тепловых машин КПД всегда ниже. Карно привел пример цикла, работая по которому, можно было бы получить максимальный КПД. Этот цикл состоит из двух изотерм (газ меняет свой объем при постоянной температуре) и двух адиабат (адиабатическим называется процесс, происходящий без обмена теплом с окружающей средой). График цикла Карно изображен на рисунке 12. На участке 1-2 газ испытывает изотермичес­кое расширение. Именно на этом участке он получает от нагревателя количество теплоты Q₁; и нагреватель и газ имеют одну и ту же температуру Т₁. Таким образом, внутренняя энергия газа на этом участке не меняется (ΔU=0), и, согласно первому началу термодинамики, совершаемая газом работа будет равна А₁=Q₁. Участок 2-3 - это адиабатическое расширение газа. Теплообмена с окружающей средой нет (ΔQ=0), работа А₂ совершается за счет уменьшения внутренней энергии газа А₂=-ΔU (снижения его температуры с Т₁ до Т₂). Точка 3 означает начало сжатия газа: сначала изотерми­чески при температуре Т₂  (холодильнику).