Учебное пособие по физике. Часть II. Молекулярно-кинетическая теория, страница 17

Объединенный газовый закон:

P=n₀×k×T

n₀ – число молекул в единице объема газа

n₀=N/V

N – общее число молекул

V – объем газа

(P×V)/T=N×k где N и k const при m const.

(P×V)/T=const

При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина, одинаковая для всех состояний этой массы газа.

P₁, V₁, T₁ – значение в начале процесса

P₂, V₂, T₂ – значение в конце процесса

(P₁×V₁)/T₁=( P₂×V₂)/T₂

 

Уравнение Клапейрона - Менделеева. Плотность газа

Выясним, какой вид будет иметь соотношение, если в него ввести молярную газовую постоянную R. Так как N-полное число молекул в массе газа m, а N_A -число молекул в одном моле, то

N=ν×NA

Где ν -число молей в массе газа m. Поэтому pV/T=ν N_A×k

Поскольку N_A×k =R, а ν равно массе газа m, деленной на массу одного моля газа u, то получаем

pV/T=(m/μ)R                               (1)

Соотношение (1) называется уравнением Клапейрона - Менделеева или уравнением состояния для произвольной массы идеального газа. Для одного моля идеального газа уравнение Клапейрона - Менделеева принимает вид

pV_моль=RT                                     (2)

С помощью формулы (1) легко выяснить, какими величинами определяется плотность газа. Так как ρ=m/V, то из (1) имеем

P= ρμ/RT                                       (3)

Зависимость средней квадратичной скорости молекул газа от температуры.

Выясним теперь, как можно с помощью вычислений находить среднюю квадратичную скорость движения молекул газа. Поскольку средняя кинетическая энергия поступательного движения молекул газа E=(3/2)kT, то можно написать mv_с.к.²/2=(3/2)kT, откуда _. Отметим, что под m в формуле подразумевается масса одной молекулы в килограммах. Так как k=R/N_a, получим v_с.к.. Поскольку  mN_A  есть масса одного моля газа μ, имеем  _.

Наконец, из (3) следует, что RT/μ=p/ρ, поэтому

                                                                        

Среднюю квадратичную скорость можно находить по любой из формул. Из функции Максвелла можно получить формулы для средней арифметической скорости и наивероятнейшей скорости. Средняя арифметическая скорость    ϋ=.

Изобарический процесс

Процессы, при которых масса газа и один из его параметров остаются постоянными, называются изопроцессами (от греческого «изос» - равный, одинаковый). Поскольку имеются три параметра газа, существуют три различных изопроцесса. Первый из них изохорический. На рисунке 1 схематически изображен опыт Гей-Люссака. Колба с газом помещается в сосуд с водой и льдом. В пробку вставлена трубка, изогнутая таким образом, что свободный конец ее горизонтален. Газ в колбе отделен от окружающего воздуха небольшим столбиком ртути в трубке. Температуру газа определяют по термометру, а объем - по положению столбика ртути. Для этого на трубке нанесены деления, соответствующие определенному внутреннему объему  трубки (при градуировке трубки можно учесть и расширение сосуда при нагревании, но оно сравнительно мало).

Сначала по положению столбика ртути l определяют V₀ - объем газа при 0ºС. Затем газ нагревают (столбик ртути перемещается в положение 2), в процессе нагревания записывают значение объема и температуры и строят график, который называют изобарой.

Оказывается, что изобара представляет собой прямую линию, которая пересекается с осью абсцисс в точке А.

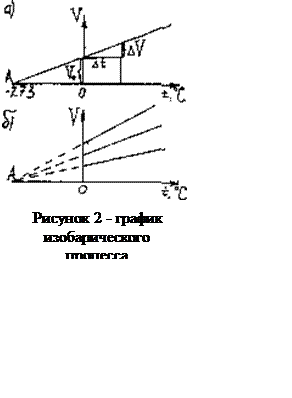Из подобия треугольников на рисунке 2 следует

V₀/OA=ΔV/Δt,

или
1/ OA=Δ/(V₀Δt).

Обозначив 1/ОА через β, получим:

ΔV=β V₀ Δt

Здесь β - температурный коэффициент объемного расширения газа.

Если повторять этот опыт для разных газов или для разных масс газа, то все графики будут пересекаться в точке А, соответствующей

t=-273ºС, т.е. коэффициент β=1/AO=(1/273)ºC^-1 одинаков для всех газов. Это означает, что расширение газа при изобарическом процессе не зависит от его природы. Процесс в газе, который происходит при постоянной массе и неизменном давлении, называется изобарическим (от греческого «барос» - тяжесть). Этот процесс был изучен французским учёным Л.Гей – Люссаком 1802г.