Прикладные методы в теории вероятности

Часть II. Прикладные методы в теории вероятности

Раздел 1. Метод наименьших квадратов

1.1. Задачи сглаживания экспериментальных зависимостей

В основе практически любых расчетных задач лежат математическ  ие модели, определяющие зависимости между теми или иными характеристиками изучаемых систем.

Математические модели позволяют предсказывать (рассчитывать) реакцию системы на возмущающее или управляющее воздействия и на этой основе решать различные задачи анализа и оптимизации этих систем.

Иногда удается строить математические зависимости, опирающиеся на фундаментальные законы природы и не требующие для своего формирования проведения экспериментов или наблюдений за изучаемыми объектами — фундаментальные модели.

Пример 1. Определение состава многокомпонентной механической смеси  в зависимости от состава компонентов  и массовых расходов  этих компонентов

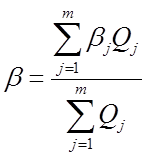                                                                                         (1.1)

Здесь фактически используется закон сохранения массы. Под составом может пониматься химический, минералогический, ганулометрический.

Пример 2. Уравнение движения материальной точки — зависимость ускорения от силы и массы

                       

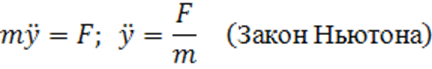
                                                                                         (1.2)

Пример 3. Зависимость электрического напряжения от силы тока и сопротивления

                                   

                                                                                         (1.3)

Чаще, однако, приходится строить концептуальные модели, которые базируются на тех или иных гипотезах (в свою очередь, ориентированных на те или иные фундаментальные законы)

Обычно такие модели определены с точностью до параметров, нахождение которых требует специального (активного) эксперимента или наблюдения за интересующим объектом в режиме нормального функционирования (пассивный эксперимент)

Пример 4. Модель смеси с учетом пылеуноса

                               

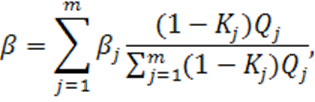
                                                                                         (1.4)

где  — коэффициент пылеуноса -ого компонента.

Здесь наряду с законом сохранения материи используется гипотеза, что унос пыли  пропорционален расходу соответствующего компонента . В этой модели  параметров , которые необходимо определять экспериментально.

Пример 5. Модель груза на пружинке и демпфера

                                                                          (1.5)

                                                   

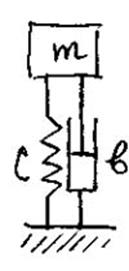
Груз массы  связан с основанием с помощью пружины жесткости  и демпфера, создающего вязкое трение и характеризуемого коэффициентом . Входным воздействием является сила , приложенная к грузу, а выходом – перемещение груза .

Здесь наряду с бесспорным законом Ньютона использована гипотеза о пропорциональности силы трения скорости и силы сжатия пружины – перемещению. Параметры  и  могут нуждаться в экспериментальном определении.

Пример 6. Модель измерений химического состава рентгеновским спектрометром.

Контролируемый образец, представляющий собой навеску постоянной массы (спрессованная или сплавленная таблетка) из предварительно измельченного анализируемого материала подвергается рентгеновскому облучению в течение фиксированного времени и по интенсивности отраженного под определенным углом излучения судят о процентном содержании определенного химического элемента или соединения. Здесь может использоваться в простейшем варианте линейная модель

                                           

                                                                                         (1.6)

где  — %-содержание химического соединения, а  — интенсивность так называемого характеристического излучения, коэффициенты которой  и  определяются экспериментальным путем.

Если учитывать так называемый матричный эффект, то необходимо строить модель вида

                                       

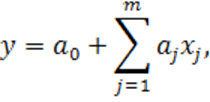
                                                                                         (1.7)

где  — %-содержание -ого химического соединения, входящего в состав анализируемого образца.

В общем виде применительно к моделям (1.4) – (1.7) речь идет о формировании математической модели зависимости  от переменных , , …, , заданной с точностью до параметров , , …,

                       

                                                                                         (1.8)

Казалось бы, для определения  параметров , достаточно провести  экспериментов, заключающихся в реализации  различных наборов входных воздействий , , …, ,  и фиксации соответствующих значений выхода модели (1.8) , . При этом получим систему  уравнений с  неизвестными , , …,

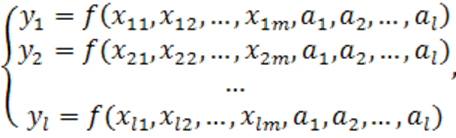
                                                                                         (1.9)

решив которую, найдем неизвестные параметры .