где 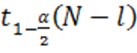 — квантиль
— квантиль ![]() –распределения с
–распределения с ![]() степенями свободы порядка
степенями свободы порядка 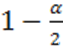 .
.
Отсюда имеем:
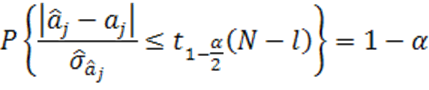
или
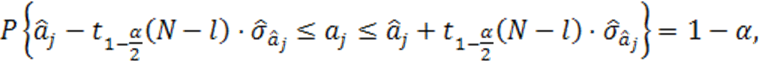
а значит, найдены границы доверительного интервала
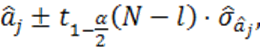
(1.59)
где
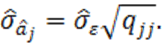
Пример.
Пусть ищутся интервальные оценки для 5-параметрической модели по
выборке из 28 точек. Доверительная вероятность составляет 0,95. В этом случае ![]() ,
, ![]() ,
, 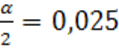 или в процентах
или в процентах 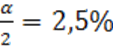 . По таблице «Процентные точки
распределения Стьюдента» (односторонняя критическая область) находим при
. По таблице «Процентные точки
распределения Стьюдента» (односторонняя критическая область) находим при ![]() ,
, ![]() .
.
Для сравнения заметим, что ![]() , т.е. при использовании более грубых
интервальных оценок, основанных на нормальном распределении, мы бы несколько
заузили доверительный интервал
, т.е. при использовании более грубых
интервальных оценок, основанных на нормальном распределении, мы бы несколько
заузили доверительный интервал ![]() по сравнению с более тонкими оценками,
основанными на распределении Стьюдента
по сравнению с более тонкими оценками,
основанными на распределении Стьюдента ![]() .
.
2.2) Интервальная оценка линейной регрессии
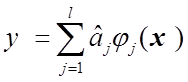 .
.
Границы доверительного интервала находятся аналогичным образом по формуле
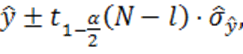
(1.60)
где
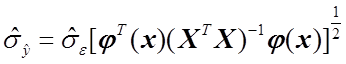 .
.
1.6. Проверка значимости оценок параметров регрессии
При построении регрессионных моделей обычно стремятся минимизировать их сложность и, в частности, при сохранении точности уменьшить число слагаемых в выражении
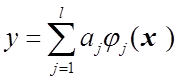 .
.
(1.61)
Поскольку на начальной стадии построения модели нередко
рассматривается избыточная структура с большим числом ![]() , то в дальнейшем возникает вопрос об
отсеивании мало значащих слагаемых, для которых коэффициенты
, то в дальнейшем возникает вопрос об
отсеивании мало значащих слагаемых, для которых коэффициенты ![]() близки к нулю.
близки к нулю.
Для этой цели, прежде всего, полезно перед построением модели выполнить нормирование переменных, т.е. приведение их к безразмерному виду и равному масштабу.
Из (1.61) следует, что
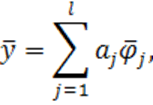 (1.62)
(1.62)
где
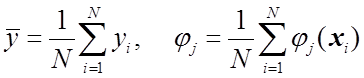 ,
,
выборочные средние
Тогда
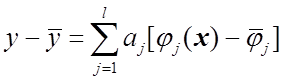 (1.63)
(1.63)
и
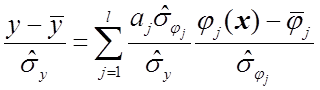 (1.64)
(1.64)
где
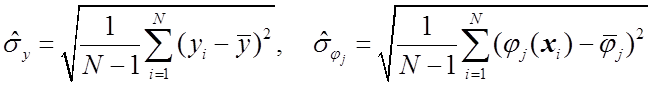
выборочные СКО.
Переходя к нормированным переменным и коэффициентам
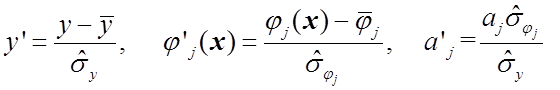 ,
(1.65)
,
(1.65)
получим искомую модель
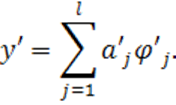 (1.66)
(1.66)
Если в нормированной модели (1.66) какие-либо коэффициенты ![]() близки к нулю, то это является определенным
основанием для «выкидывания» из нее соответствующих слагаемых, т.е. признания
их незначимыми.
близки к нулю, то это является определенным
основанием для «выкидывания» из нее соответствующих слагаемых, т.е. признания
их незначимыми.
Для обоснованного удаления таких слагаемых из модели следует
выполнить для каждого из них проверку гипотезы о том, что соответствующий
параметр ![]() равен нулю. Такая гипотеза может быть
принята, если доверительный интервал
равен нулю. Такая гипотеза может быть
принята, если доверительный интервал
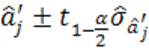
при малой выборке или
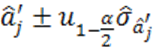
при большой выборке «накрывает» (содержит) значение ![]() .
.
Пример 1.
Пусть ![]() ,
, 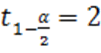 ,
, 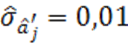 . В этом случае интервал
. В этом случае интервал ![]() не содержит нулевое значение, а значит
не содержит нулевое значение, а значит ![]() -е слагаемое модели удалять не следует.
-е слагаемое модели удалять не следует.
Пример 2.
Пусть ![]() ,
, 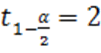 ,
, 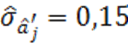 . В этом случае интервал
. В этом случае интервал ![]() содержит нуль, а значит
содержит нуль, а значит ![]() -е слагаемое может быть удалено из модели.
-е слагаемое может быть удалено из модели.
После удаления незначимых параметров можно легко найти параметры ненормированной модели с помощью соотношений (1.65).
1.7. Оценка качества регрессионной модели
Основное назначение регрессионных моделей — достаточно точное
предсказание выходной переменной
y по значениям
входов x.
Обычно для построения модели необходимо потратить много усилий и средств,
поэтому, построив модель, важно понять, в какой степени она помогла снизить
неопределенность при оценивании y. При этом можно рассуждать следующим образом. В
отсутствие модели в качестве оценки yможно принять его среднее значение ![]() . Тогда рассогласование между
экспериментальными данными
. Тогда рассогласование между
экспериментальными данными ![]() и подобной наиболее
простой моделью может быть задано оценкой СКО y
и подобной наиболее
простой моделью может быть задано оценкой СКО y
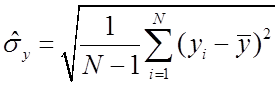 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.