Прикладные методы в теории вероятности, страница 10

                                                

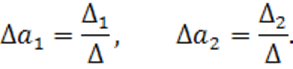
Будем оценивать точность модели комплексным показателем

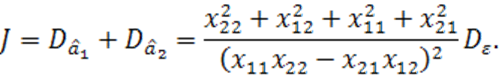                                              (1.76)

Каждый эксперимент может быть охарактеризован вектором

                                                  .

Соответственно, план серии из двух экспериментов может быть задан парой векторов. Рассмотрим несколько подобных планов, предполагая, что существуют ограничения на входные воздействия

Различные планы иллюстрируются рисунками.

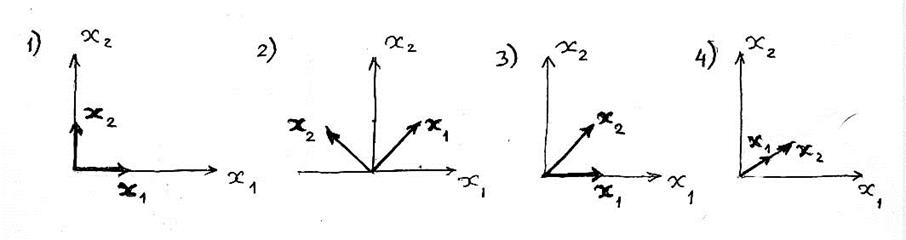
План 1:

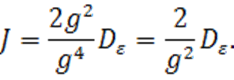
Ясно, что

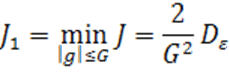
при .

Заметим, что вектора  и  ортогональны, т.е.

.

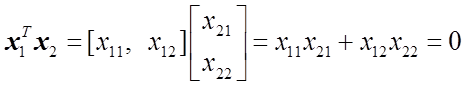План 2:

Этот план эксперимента также ортогональный.

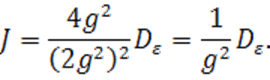
Ясно, что

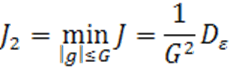
при .

Заметим, что как и в первом плане  .

План 3:

Уменьшим угол между векторами  и .

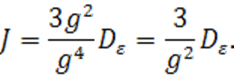
Ясно, что

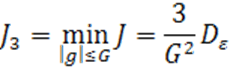
при .

План 4:

Рассмотрим случай, когда вектора  и  коллинеарные, т.е. =k.

В этом варианте

      

а значит .

Выводы.

1. Качество МНК оценок тем лучше, чем ближе план эксперимента к ортогональному. В общем случае для модели 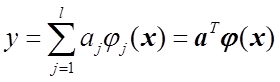 условие ортогональности имеет вид

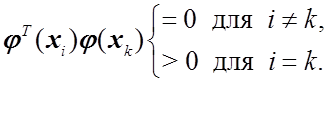
Качество МНК оценок тем лучше, чем больше по модулю входные воздействия .

Оптимизация входных воздействий из условия минимизации ошибок модели — предмет теории планирования эксперимента. Одна из постановок

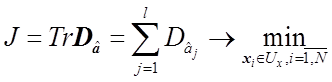
2. Качество МНК оценок тем хуже, чем ближе выборка данных, по которым строится модель, к условиям мультиколлинеарности, т.е.  линейной зависимости входных воздействий, когда для какого либо входа   выполняется условие

,

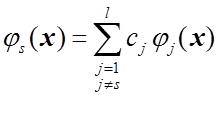где хотя бы один коэффициент  отличен от нуля.

Действительно, в этом случае для суммы квадратов невязок выполняется соотношение

,

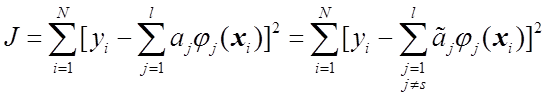где

                                                                           (1.76’)

а следовательно, минимизация этой суммы по a не может дать однозначного решения, т.к. определив по МНК , можно задавая различные значения , получать из (1.76’) соответствующие значения .

Явление мультиколлинеарности при построении моделей множественной регрессии может иметь место в условиях пассивного эксперимента.

Типичные ситуации:

1. Функциональная или статистическая зависимость между некоторыми входами, возникающая из-за того, что на каждый из них оказывает влияние некий фактор, не включенный в модель. Например, заметив, что курс доллара на московской бирже зависит от курса доллара предшествующих торгов токийской и нью-йоркской бирж, можно построить регрессионную модель для прогноза курса доллара в Москве по данным о курсе в Нью-Йорке и Токио. Однако эта модель может оказаться неустойчивой, т.к. курс на токийской и нью-йоркской биржах зависит от индекса Доу-Джонса.

В подобной ситуации следует выявить взаимозависимые факторы путем подсчета коэффициентов парной корреляции входных воздействий и уменьшить число входов настолько, чтобы оставшиеся входы были слабо коррелированны между собой (при этом, однако, надо следить за точностью модели). Для формализованного решения задачи выбора минимального числа наиболее информативных входов служит, например, метод главных компонент.

2. Модель управляемого процесса по данным нормальной эксплуатации. Например,

где  — управляющее воздействие, а  — неконтролируемое возмущение.

          Пусть задача стабилизации состоит в поддержании yна нулевом уровне. При стабилизирующем управлении  возникает ситуация линейной зависимости между входами модели. В отличие от первого случая целью моделирования является не прогнозирование выхода , а определение оценок параметров. Зная эти оценки, можно эффективно скомпенсировать возмущения, определив из условия значение коэффициента усиления 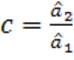. Следовательно, в данной ситуации сокращение числа входов модели не является средством решения проблемы коллинеарности. Для этого необходимо ввести элементы активного эксперимента, дополнив сигнал управления  специальной, не зависящей от , составляющей , в допустимой степени «раскачивающей» исследуемый объект.