Прикладные методы в теории вероятности, страница 2

Действительно, так и следует поступать в детерминированных условиях, характеризуемых свойствами повторяемости экспериментов, когда при одинаковом наборе значений входов модели , мы всегда получаем те же значения . Это условие, однако, выполняется далеко не всегда как в силу погрешностей контроля переменных, так и в силу учета в реальных моделях всех факторов, влияющих на выходную переменную.

Из рассмотренных примеров концептуальных моделей (примеры 4-6) на достаточную степень детерминированности, по-видимому, можно рассчитывать только в примере 5. В примере 4 при фиксации входов  разброс выхода  обычно вызван значительными погрешностями контроля химического состава и расходов, неточностью самой гипотетической зависимости , проявляющейся как в отсутствии учета нелинейности, так и в непостоянстве коэффициента пылеуноса , зависящих, например, от параметров аэродинамического режима в смесительном агрегате.

В частности, в примере 6 разброс данных обусловлен целым рядом причин: неточность навески, различия анализируемых  образцов из-за вариаций режима подготовки таблеток, изменения режима эксплуатации рентгеновской трубки, отсутствие учета матричного эффекта в одномерном варианте модели (1.6). В итоге экспериментальные точки на диаграмме рассеяния не лежат на прямой, соответствующей графику линейной зависимости (1.6), и желательно провести модельную прямую так, чтобы она, по возможности, проходила как можно ближе ко всем экспериментальным точкам.

                        

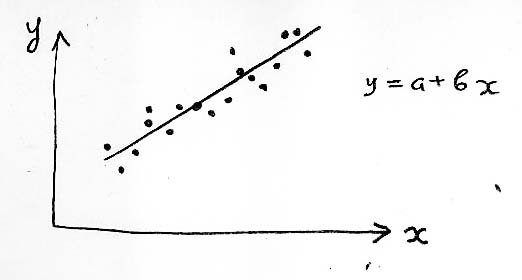
1.2. Расчет параметров моделей по методу наименьших квадратов

Суть подхода состоит в том, чтобы использовать для определения  параметров модели (1.8) не , а, как правило, гораздо большее число  экспериментов и затем с применением их результатов свести задачу определения параметров к некоторой задаче оптимизации.

Для сокращения записи формул введем векторные обозначения, а именно:

                            .

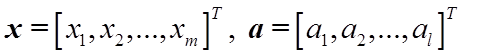Тогда (1.8) запишется в виде

                                                 .

                                                                                       (1.10)

Результаты -ого эксперимента , , …,  будем обозначать , . Введем также в рассмотрение рассогласования

                                            

                                                                                       (1.11)

между модельным  и измеренным  выходами изучаемого процесса и постараемся выбрать значения неизвестных параметров  таким образом, чтобы минимизировать по модулю  для всех .

Формализация высказанной идеи может быть различной. Например, можно решать задачу

                                                   

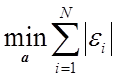
или

                                                                  ,

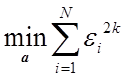где  — любое натуральное число, однако наибольшее распространение получил  метод наименьших квадратов (МНК), разработанный в 19-м веке немецким математиком Гауссом. В рамках МНК  ищется из условия минимизации функции

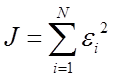
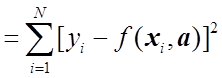                                          .                            (1.12)

Покольку речь идет о поиске экстремума функции  переменных , , …, , то необходимое условие экстремума заключается в обращении в нуль частных производных минимизируемой функции

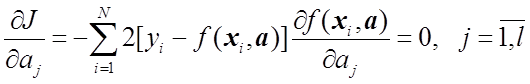                                 (1.13)

Таким образом, в общем случае задача сводится к решению системы  нелинейных уравнений относительно  неизвестных, компонентов вектора . Это весьма сложная проблема, так что чаще имеет смысл непосредственно решать задачу (1.12) с использованием одного из известных методов поисковой оптимизации (варианты методов перебора, градиентные процедуры, метод наискорейшего спуска и другие).

Вместе с тем, огромная популярность МНК определяется простотой нахождения  для весьма широкого класса моделей, линейных по параметрам, а именно

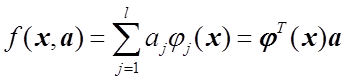                           ,                                (1.14)

где

                             .