Прикладные методы в теории вероятности, страница 3

Для таких моделей приходим к задаче нахождения

                                   

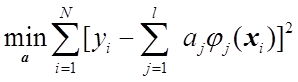
                                                                                       (1.15)

или                   

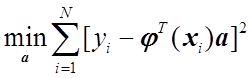                                                  .                                (1.16)

Для компактной записи решения введем вектор измерений выходной переменной

                                         ,

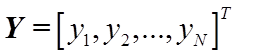а также матрицу измерений входных переменных

                             

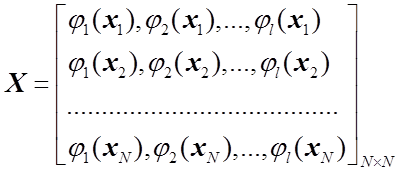
.                                                                                      (1.17)

Тогда, если бы модель (1.14) точно соответствовала измерениям Y, то было бы

                                              

                                                                                       (1.18)

но поскольку, вообще говоря, такого соответствия нет, то избыточная по числу уравнений система (1.18) решается путем минимизации квадратичной функции невязок (1.15), которая может быть записана в виде

      

                                                                                       (1.19)

Записывая условия минимизации с учетом правил дифференцирования скалярного произведения векторов

                                      

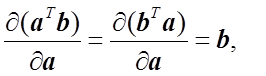
                                                                                       (1.20)

получим

                               ,

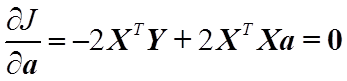откуда

                                               

                                                                                       (1.21)

( — так называемая информационная матрица Фишера) и

                                         

                                                                                       (1.22)

Таким образом, по МНК параметры модели (1.14) находятся путем решения системы линейных алгебраических уравнений (так называемой системы нормальных уравнений)

                       ,

                                                                                       (1.23)

где

       ,

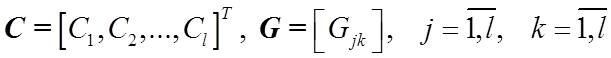причем

,

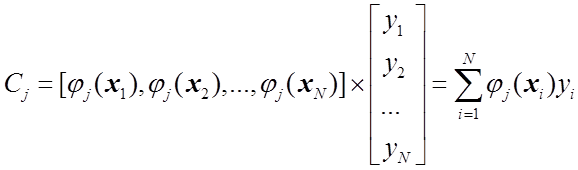                                                                                                             (1.24)

.

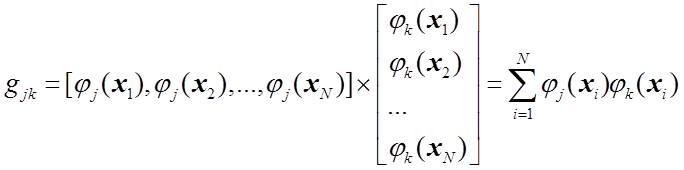В большинстве расчетных задач, связанных с анализом или оптимизацией систем, переменные изменяются в относительно узком диапазоне. При этом монотонные зависимости хорошо аппроксимируются линейными функциями, а экстремальные — квадратичными функциями.

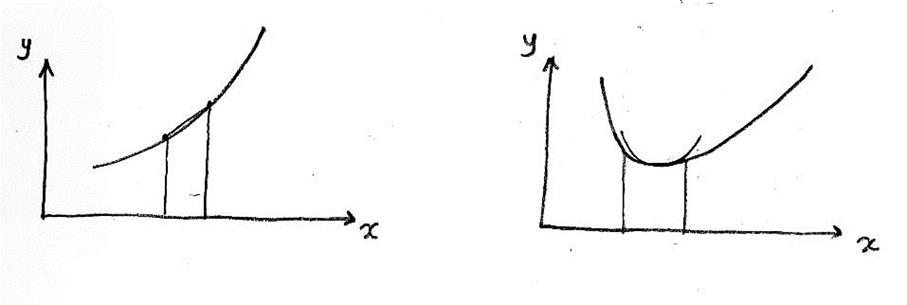
Отсюда следует особая роль линейных моделей:

(одномерная модель)

                                                                                       (1.25)

(многомерная модель)

                                                                                       (1.26)

и квадратичных моделей:

(одномерная модель)

                                                                                       (1.27)

(многомерная модель)

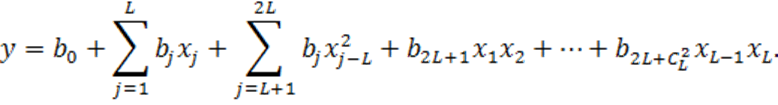
                                                                                       (1.28)

Все они представляют собой частный случай линейной по параметрам модели (1.14). Например, полагая

получим для определения коэффициентов  линейной по x многомерной модели (1.26) систему уравнений

                                              

где

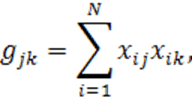
                                                                                       (1.29)

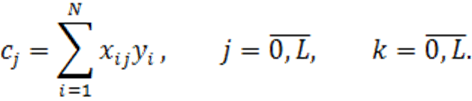
                                                                                       (1.30)

Для одномерного варианта линейной модели (1.25) несложно получить конечные соотношения для расчета коэффициентов модели  и .

В этом случае

                                    

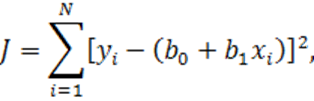
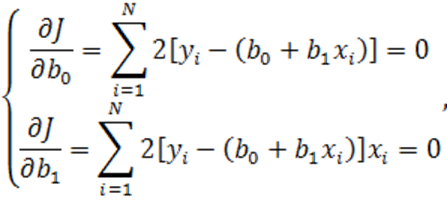
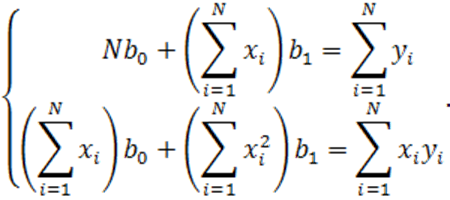
                                                                                       (1.31)

Вводя обозначения

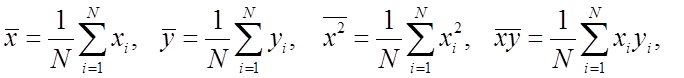
запишем систему уравнений (1.31) в виде

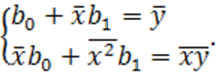
                                                                                       (1.32)

Отсюда получим оценку параметра :