Прикладные методы в теории вероятности, страница 5

Оно, например, происходит из-за неполной достоверности гипотез, принятых для описания моделируемых явлений. Так, при отсутствии точных представлений об изучаемом объекте, исходят из априорных гипотез о гладкости идентифицируемых зависимостей, приближая их линейной формой или формой второго порядка, что, разумеется, сопряжено с погрешностями.

2) Факторы неопределенности в результате измерений.

Имеется два основных источника неопределенностей:

а) Случайные ошибки измерений .

б) Наличие неучтенных или (и) неконтролируемых факторов, влияющих случайным образом на  помимо x .

Допущения, которые кладутся в основу вероятностного обоснования МНК, предполагают отсутствие искажения формы регрессионной зависимости, то есть предполагается, что существуют значения параметров a, называемые истинными, такие, что при отсутствии факторов неопределенности зависимость  точно описывает функциональную связь между x и  для всех наблюдаемых значений x.

Кроме того, делается ряд допущений относительно случайных отклонений  экспериментальных данных  от истинных значений   , а именно:  считаются независимыми (для разных ) нормально распределенными случайными величинами с нулевым математическим ожиданием и одинаковыми; хотя, как правило, заранее неизвестными, дисперсиями .

Покажем, что при сделанных допущениях оценки по методу МНК соответствуют оценкам по методу максимального правдоподобия (ММП), который имеет ряд достоинств. В частности, ММП-оценки обладают свойством эффективности в классе асимптотически нормальных оценок .

Смысл оценок по ММП состоит в следующем.

Пусть имеется случайная величина  с распределением, которое зависит от вектора параметров a, который неизвестен и нуждается в определении.

Имея результаты измерений выходной переменной 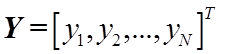естественно в качестве оценки вектора параметров 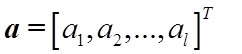взять значения , доставляющие максимум условной плотности вероятности , т.е. наиболее вероятные апостериорные значениия параметров модели. Но по формуле Байеса

                               

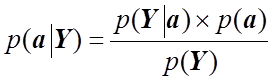
                                                                                       (1.37)

Таким образом, видно, что апостериорная плотность вероятности пропорциональна априорной , умноженной на так называемую функцию правдоподобия . В предположении, что различные значения a равновероятны, что эквивалентно допущению о том, что в области возможных значений a     , приходим к выводу, что задача максимизации неизвестной функции  эквивалентна задаче максимизации функции правдоподобия .

Поскольку , где  при фиксированных  и a не случайная величина, а , то отсюда следует, что , а тогда

                                   .

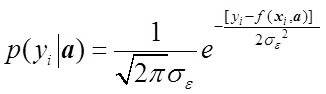                                                                                       (1.38)

Поскольку предполагалась взаимная независимость  (для различных ), то

            

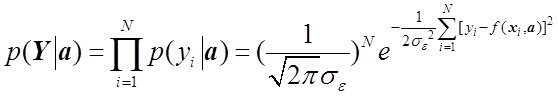
                                                                                       (1.39)

Отсюда прямо следует, что задача 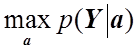 эквивалентна задаче

                                      ,

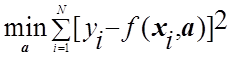что и требовалось доказать.

Заметим, что при различных дисперсиях измерений в разных точках

                 ,

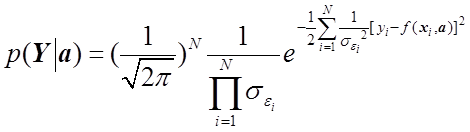                                                                                       (1.40)

откуда получаем модифицированный для этого случая критерий МНК

                               

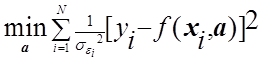
                                                                                       (1.41)

1.4. Вероятностные свойства оценок метода наименьших квадратов

1) Несмещенность: .

Доказательство:

В соответствии с (1.22) .

Тогда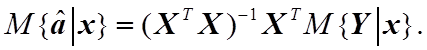

Поскольку , то 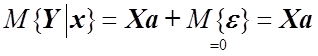 и после подстановки в предыдущую формулу получим

                    

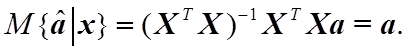
2) Состоятельность:  при .

Доказательство.

         

                                                                                       (1.42)

Отсюда

                             

                                                                                       (1.43)