Прикладные методы в теории вероятности, страница 4

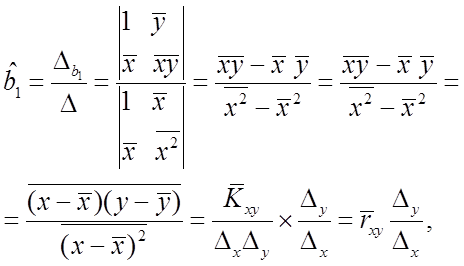
                                                                                       (1.33)

где дополнительно введены обозначения для выборочного коэффициента корреляции

                                

нормированного выборочного коэффициента корреляции

                                           ,

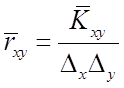а также выборочных дисперсий

                         

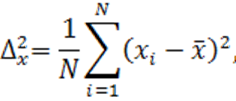
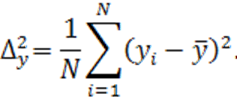
Оценку коэффициента  находим непосредственно из первого уравнения системы (1.32)

                                         

                                                                                       (1.34)

Заметим, что определитель системы (1.32)

                        

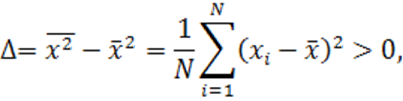
                                                                                       (1.35)

если среди значений , , …,  есть различные. В этом случае система (1.32) имеет единственное решение.

Стандартным способом приведения нелинейных моделей к линейным по параметрам является разложение в ряд Тейлора, как правило, с точностью до первого (линейные по  модели (1.25), (1.26)) или до второго (квадратичные по  модели (1.27), (1.28)) порядка малости

    

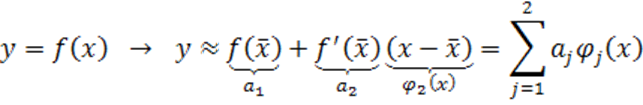
или

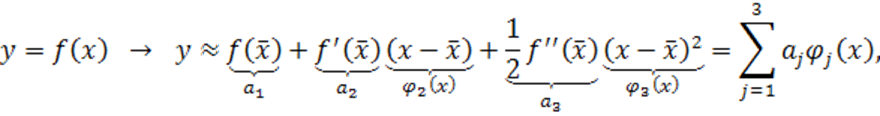
где .

Поскольку такая аппроксимация нелинейных зависимостей приводит к заведомо приближенным моделям, то при возможности следует использовать особые приемы линеаризации по параметрам, не связанные с потерей точности.

Пусть, например, необходимо определить параметры  и  зависимости

                                                   

Тогда, логарифмируя, получим

                                    

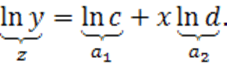
После того, как найдем коэффициенты  и  линейной по параметрам модели из условия минимизации

                                     ,

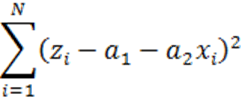определим исходные параметры

                                  

Приведем несколько других примеров, сведя их в таблицу

Исходная функция	Преобразованная функция

Еще один пример – тригонометрическая модель .

1. Сначала рассмотрим вариант, когда известны время t и частота колебаний ω, а не известны и нуждаются в оценке амплитуда A и фаза колебаний φ.

          Модель нелинейна по φ. Запишем ее в виде

                                       

и обозначим

                        

Таким образом приходим к линейной по параметрам модели .

Обратный переход после получения с помощью МНК оценок  и  выполняется по формулам

                                          .

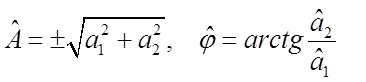Уточнить знак можно из соотношения .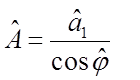

2. Пусть теперь и ω не известна и нуждается в оценке. Тогда дважды продифференцировав исходную модель по t, получим соотношение

                                             .

Обозначив  найдем a путем минимизации

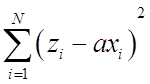, а тогда . После нахождения ω можно найти оценки A и φ так, как это сделано в п.1.

1.3. Вероятностное обоснование метода наименьших квадратов

Популярность МНК связана не только с простотой расчета параметров моделей, но и с возможностью его вероятностного обоснования как, при определенных условиях, наилучшего метода оценки параметров. Подобное обоснование позволяет также оценить точность получаемых моделей.

В вероятностной трактовке МНК предполагается, что существуют зависимости вида , отражающие связь между x и y лишь в среднем. Более конкретно, , то есть зависимость  представляет собой условное математическое ожидание выхода модели  при значениях входов x. В отличие от функциональных зависимостей такие зависимости называются регрессионными. Задача МНК при этом состоит в нахождении оценок параметров регрессионных моделей.

Вообще говоря, существуют два основных источника неточностей экспериментально-статистических моделей, проявляющихся в том, что

                                       

                                                                                       (1.36)

1) Искажение формы истинной зависимости.