Если же построить модель 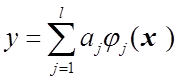 и с ее помощью получать оценки
и с ее помощью получать оценки 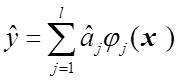 , то рассогласование между
экспериментальными данными
, то рассогласование между
экспериментальными данными ![]() и такой моделью может
быть задано оценкой СКО измерительных ошибок ε
и такой моделью может
быть задано оценкой СКО измерительных ошибок ε
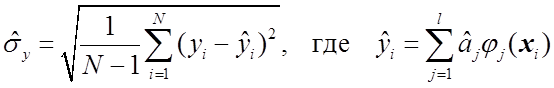 .
.
Показателем качества регрессионных моделей (то есть их способности
снижать неопределенность при прогнозе y) служит так называемая мера
неопределенности модели, выражаемая отношением оценок СКО ошибки модели ![]() и выходной переменной
и выходной переменной ![]()
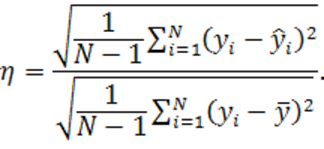 (1.67)
(1.67)
Можно показать, что если модель ищется в виде (1.61), то
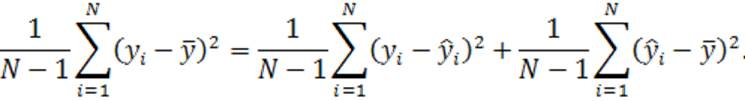
(1.68)
Отсюда следует, что
![]() (1.69)
(1.69)
причем, чем качественнее модель, тем ближе ![]() к нулю.
к нулю.
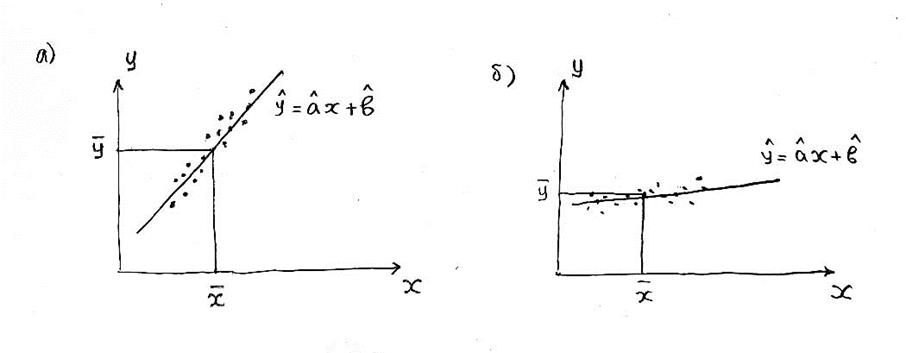
Для однофакторных моделей с одним входом ![]() достаточно хорошее представление о
качестве аппроксимации экспериментальных данных дает диаграмма рассеяния с
нанесенным на нее графиком полученной регрессионной модели. На рисунке показаны
два типичных случая. В варианте а) модель обладает более высоким качеством, чем
на рисунке б).
достаточно хорошее представление о
качестве аппроксимации экспериментальных данных дает диаграмма рассеяния с
нанесенным на нее графиком полученной регрессионной модели. На рисунке показаны
два типичных случая. В варианте а) модель обладает более высоким качеством, чем
на рисунке б).
Часто для оценки качества модели используется также так называемый коэффициент множественной детерминации
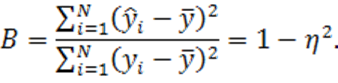 (1.70)
(1.70)
Очевидно, что ![]() , причем чем ближе
, причем чем ближе ![]() к
к ![]() , тем более модель детерминирована, т.е.
тем меньшую роль играют случайные факторы.
, тем более модель детерминирована, т.е.
тем меньшую роль играют случайные факторы.
1.8. Влияние входных воздействий на качество регрессионных моделей
Ранее было получено соотношение 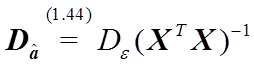 , из
которого следует, что точность оценки параметров по МНК зависит от значений
входных воздействий в выборке, по которой построена регрессионная модель. Этот
общий вывод иллюстрируется рисунком.
, из
которого следует, что точность оценки параметров по МНК зависит от значений
входных воздействий в выборке, по которой построена регрессионная модель. Этот
общий вывод иллюстрируется рисунком.
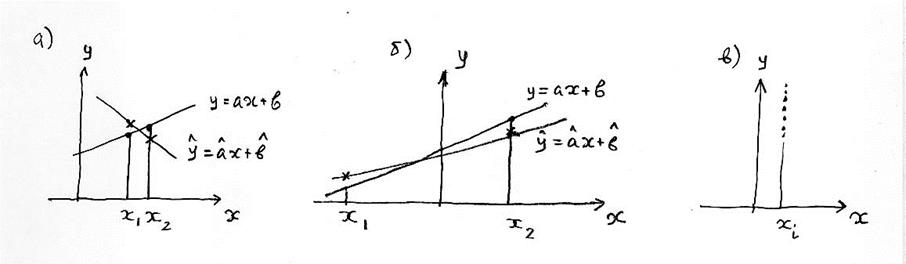
На рис. а) и б) показаны оценки линейной зависимости y от x, полученные по данным двух экспериментов со значениями входной переменной x1 и x2 . Видно, что в присутствии измерительных ошибок существенное значение имеет расположение точек x1 и x2. В случае а) они расположены близко, и модель получилась плохая. В случае б) точки разнесены на большое расстояние, и полученная модель гораздо ближе к истинной зависимости. В случае в) все точки xi совпадают, при этом модель построить не возможно.
Если модель строится по данным активного эксперимента, то выбирая входные воздействия оптимальным образом, можно максимизировать точность оценки параметров. Если модель строится по данным пассивного эксперимента, когда входные воздействия могут лишь контролироваться, но не подлежат целенаправленным изменениям, то в неблагоприятных ситуациях возможна существенная потеря точности МНК вплоть до полной потери его работоспособности.
Рассмотрим типичные ситуации на простом примере. Пусть необходимо
определить параметры ![]() и
и ![]() регрессионной модели
регрессионной модели
![]()
(1.71)
по данным двух зашумленных измерительными помехами экспериментов ![]()
![]()
(1.72)
![]()
В этом случае в соответствии с МНК необходимо минимизировать
![]() (1.73)
(1.73)
и оценки ![]() и
и ![]() находятся решением системы уравнений
находятся решением системы уравнений
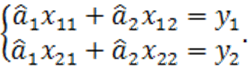
(1.74)
Из (1.72) и (1.74) получим систему уравнений для ошибок оценивания
параметров ![]() и
и ![]()
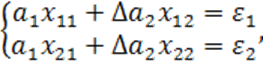 ,
,
(1.75)
откуда находим
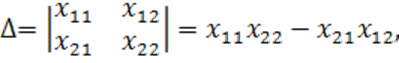
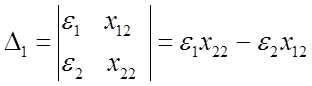 ,
,
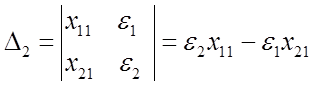
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.