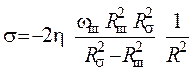 ,
(49)
,
(49)
где Rш – радиус шара, Rб – расстояние от центра шара до стенки барабана, wш – угловая скорость шара, h – вязкость обрабатываемого вещества. При этом Rш <R<Rб.
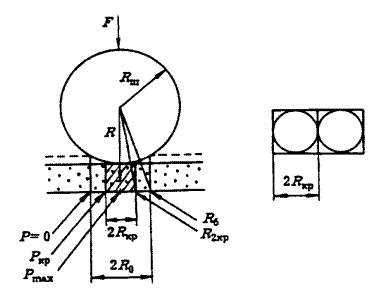
Рис. 9.Схема
обработки вещества в планетарно-центробежной мельнице
при реализации пристеночного движения шаров в барабане
Наиболее корректным выражением для определения вязкости порошка является формула Дохерти–Кригера [65]:
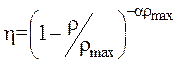 , (50)
, (50)
где r – плотность вещества, rmax – максимальная плотность вещества,
при которой h = ![]() ; a =
2.5; (rmax , равное 0.65, соответствует плотной
случайной упаковке).
; a =
2.5; (rmax , равное 0.65, соответствует плотной
случайной упаковке).
Для определения r используем закон Бальшина об изменении плотности вещества в зависимости от оказываемого на него давления [66]:
![]() , (51)
, (51)
где Pn – давление прессования, Pmax – давление прессования, соответствующее максимальному уплотнению вещества, b = rmax/r; L – фактор прессования. Отсюда
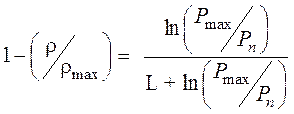 . (52)
. (52)
При R = Rб из (49), (50), (52) следует:
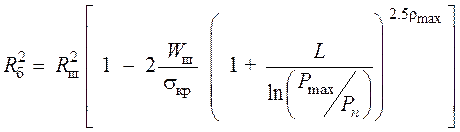 , (53)
, (53)
Rб в данном случае определяет оптимальный объем загружаемого в барабан вещества при условии, что все частицы вещества, попавшие в область между стенкой барабана и шаром, раскалываются под действием силы трения s = sкр.
Теперь рассмотрим случай,
когда число шаров в барабане равно Nш. Аналогом одного удара
в модели бинарных столкновений в данном случае будем считать перекатывание шара
(шаг) на расстояние 2Rкр, при условии, что площадь поверхности
соприкосновения шара с веществом составляет S1 = 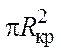 (рис. 9). Тогда общее число таких шагов i, совершенное
Nш шарами за время t, равно
(рис. 9). Тогда общее число таких шагов i, совершенное
Nш шарами за время t, равно
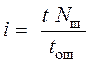 , (54)
, (54)
где tош – время одного перекатывания шара на расстояние 2Rкр. Выражение для tош определяется из уравнения
2Rкр = Rш wш tош, (55)
где wш= çw1 – w2ç, w1 – угловая скорость водила мельницы, w2 – угловая скорость барабана, и записывается в виде
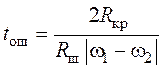 . (56)
. (56)
Тогда выражение (64) принимает вид
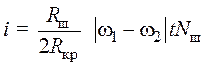 . (57)
. (57)
По аналогии с моделью бинарных столкновений [46] полагаем, что n – общее число частиц в барабане; n1 – общее число частиц радиусом rmax, попавших в зону объемом V0 = S0 (Rб – Rш), где S0 – площадка контакта радиусом R0, за пределами которой P = 0, а (Rб – Rш) – толщина слоя обрабатываемого вещества (рис. 9). По аналогии с моделью бинарных столкновений [46], число частиц n1 определяется выражением:
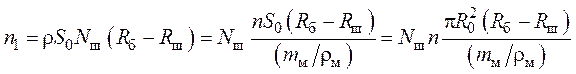 , (58)
, (58)
где r = n/V0 = n/(mм
/rм) – плотность частиц в объеме V0 , mм
и rм – масса и плотность обрабатываемого вещества
соответственно. Тогда
nр = kn1 – число частиц, расколовшихся до
радиуса rmin (k < 1), в объеме V1
= S1 (R2кр – Rш ), где S1
– площадка контакта с радиусом Rкр, на границе которой развивается
критическое давление Pкр, необходимое для разрушения частиц,
а в ее центре – максимальное Pmax (Pmax
>Pкр);
(R2кр – Rш) – толщина слоя вещества (рис. 9).
Значение nр можно записать в виде:
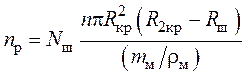 , (59)
, (59)
а число нерасколовшихся частиц, попавших в пространство вне зоны S1 , но в пределах зоны S0 , через i перекатываний шара (шагов):
![]() . (60)
. (60)
Тогда уравнение для площади внешней
поверхности [46] при
nр = n – n0i примет вид:
![]()
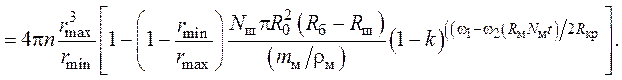 (61)
(61)
Значение R0, согласно [51], определяется выражением
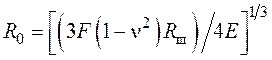 , (62)
, (62)
где F – сила воздействия на шар, равная mшg; E – модуль Юнга; n – коэффициент Пуассона [51]. Преобразуем уравнение (71), полагая, что
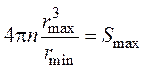
при t = 0, обозначив:
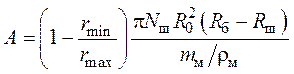 . (63)
. (63)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.