Механохимические аппараты и методы оценки их эффективности: Учебное пособие, страница 13

Графическое изображение функции (10) представлено на рис. 5.

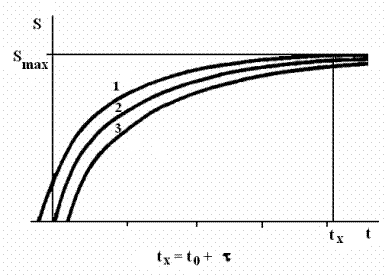
Рис. 5. Графическое изображение функции (20)
при t₀>0 (1), t₀ = 0 (2) t₀<0 (3)

Величина k₁ определяется отношением числа частиц, попавших в объем lS₁ к числу частиц в объеме lS₀ :

k₁ = rlS₁ /(rlS₀) = S₁ /S₀,                                        (11)

где S₁ – площадка контакта, на границе которой развивается критическое давление P_кр, необходимое для разрушения частиц, а в центре развивается максимальное давление P_max > P_кр .

Из [51] известно, что

P_кр = P_max [1 – (S₁ /S₀)]^1/2.                                    (12)

Комбинируя с (11), получим

     1 – k₁ = P²_кр / P²_max.                                                (13)

При этом максимальное давление в зоне контакта можно записать как

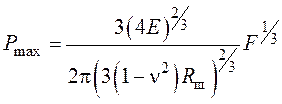    ,                                        (14)

где Е – модуль Юнга, n – коэффициент Пуассона, F – сила воздействия на шар, которая определяется из уравнения τ_o F = 2 M_ш u_ш. Здесь M_ш – масса шара, u_ш – скорость шара, а τ_o – общая продолжительность удара, определенная в работе [51]:

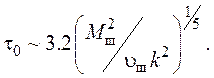                                                   (15)

Заменив k = 4/3 R_ш ^1/2 (E/1 – n²), получим

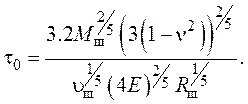                                               (16)

Тогда сила воздействия

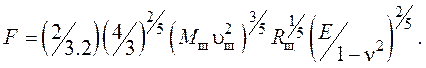                      (17)

Отсюда

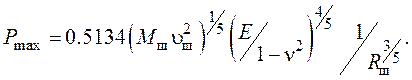                         (18)

Поскольку критическое давление, при котором происходит разрушение материала, есть величина постоянная и характерная для каждого конкретного вещества (константа), обозначим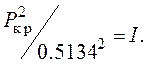

Тогда

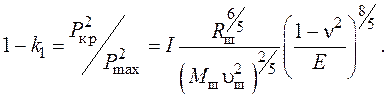                             (19)

Поэтому в уравнении (20) параметры принимают вид:

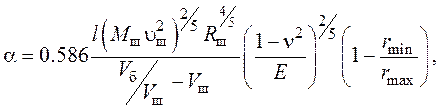                      (20)

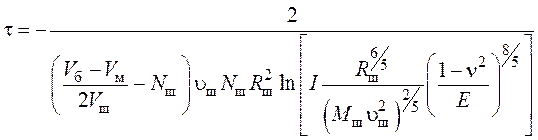    .   (21)

Длину свободного пробега определим как l = (V_б – 2N_шV_ш – V_м)^1/3. Значения величины 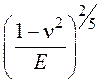 = k для МоО₃ и WO₃ для всех типов используемых мельниц были вычислены с использованием экспериментальных результатов [43] (см. табл. 3). Оказалось, что даже для одного материала эти величины не постоянны и зависят от типа мельницы.

Таблица 3

Изменение механических характеристик оксидов в зависимости от типа мельницы

Мельница
	MoO3	WO3
АГО-2	1.5×10-2	1.65×10-2
АПФ	0.72×10-2	0.72×10-2
FRITSCH	6.35×10-2	6.31×10-2

В рамках используемой модели обнаружено [45], что механические параметры МО материала зависят от типа используемой мельницы. Если меняются механические свойства материала, то меняется и сам материал, другими словами, происходит химическая реакция. Эти данные позволяют предположить существование зависимостей между механическими параметрами обрабатываемого материала и константами химических реакций, происходящих при механическом воздействии.

Таким образом, получено [45] математическое выражение (20), описывающее изменение величины внешней поверхности механически обработанного материала. При этом параметры a и t зависят от условий МО (числа шаров, их массы, радиуса и скорости), от объема барабана, от исходных и конечных размеров измельчаемых частиц и их механических параметров (модуля Юнга и коэффициента Пуассона) (см. уравнения (20), (21)). Показано, что полученную модель можно применять для оценки эффективности различных мельниц. В качестве критерия оценки используется скорость достижения максимальной величины поверхности – u = 1/t с ^-1. Теоретически построенные модели, по оценкам авторов [45], совпадают с экспериментальными результатами с точностью до некоторой константы, которая определяется из экспериментальных данных.

В табл. 4 приведены значения u = 1/t, t₀ = tlna для оксида молибдена, механически обработанного в мельницах трех типов (АГО-2, АПФ и FRITSCH) в «стандартных» условиях диспергации.

Таблица 4

Параметры модели^а) для оксида молибдена при МО в различных аппаратах в «стандартных» условиях^б)

Параметр	АГО-2	Мельница АПФ	FRITSCH
Nопт, шт	136	595	35
u, с-1	0.068	0.026	0.003
t0, c	2.9	–6.3	24.3
tx, c	17.5	32.5	421.3